Контрастирование (редукция) нейронной сети
Значимость параметров и сигналов. Сокращение описания (контрастирование) сетей.
Сокращение множества параметров и входных сигналов обученной нейронной сети преследует цели:
- упрощение специализированных устройств;
- сокращение объема используемой памяти и увеличение быстродействия;
- удешевление сбора данных;
- обеспечение (или облегчение) интерпретации результатов обработки данных.
Существует два способа сокращения (редукции) описания:
- редукция "снизу вверх" - постепенное удаление параметров от наименее значимых к более значимым;
- редукция "сверху вниз" - выделение наиболее значимых параметров и постепенное дополнение их менее значимыми.
Способ редукции "снизу вверх":
- определяются наименее значимые параметры и устраняются вместе с соответствующими элементами системы;
- оставшиеся параметры модифицируются так, чтобы наилучшим способом решить задачу;
- циклически повторять пп. 1-2 до тех пор, пока задача не будет решаться с удовлетворительной точностью.
Определение значимости параметров на основании функции оценки
Есть набор 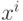 ,
, 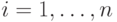 размерности
размерности  -мерный вектор параметров
-мерный вектор параметров  и
функция оценки
и
функция оценки 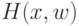 , оценивающая работу системы с параметрами
, оценивающая работу системы с параметрами  на
векторе
на
векторе  (например, расстояние от вектора выходных сигналов
системы до
нужного ответа или до множества правильно интерпретируемых ответов).
Требуется выделить наименее значимые параметры
(например, расстояние от вектора выходных сигналов
системы до
нужного ответа или до множества правильно интерпретируемых ответов).
Требуется выделить наименее значимые параметры 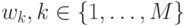 и компоненты
данных
и компоненты
данных  и модифицировать систему, отбрасывая наименее значимые
параметры. Процедура отбрасывания неоднозначна. Простейший вариант -
обращение в ноль - не всегда лучший: он не учитывает корреляции между
данными. Учитывая корреляцию, следует отбрасываемые компоненты заменять на
функции остающихся компонент.
и модифицировать систему, отбрасывая наименее значимые
параметры. Процедура отбрасывания неоднозначна. Простейший вариант -
обращение в ноль - не всегда лучший: он не учитывает корреляции между
данными. Учитывая корреляцию, следует отбрасываемые компоненты заменять на
функции остающихся компонент.
Пусть для каждого 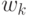 определено фиксированное значение
определено фиксированное значение 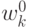 . Отбрасывание
. Отбрасывание  -ой компоненты для
-ой компоненты для  -го примера означает
приравнивание
-го примера означает
приравнивание 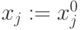 . В
качестве простейшего варианта примем
. В
качестве простейшего варианта примем  и для любого
и для любого  полагаем
полагаем
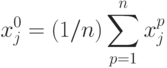
(параметры обращаются в ноль, данные заменяются средним по выборке). Более тонкие методы предполагают замену отбрасываемых параметров и сигналов на некоторые функции оставшихся.
