Модели нейронов
Сигма-Пи нейроны
Выше были рассмотрены нейроны с линейной и квадратичной функциями
активации. Сигма-пи нейроны являются их обобщением на случай представления
функции активации u полиномом степени  ,
,  - число
входов нейрона:
- число
входов нейрона:
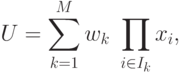
где  - множество индексов, содержащее одну из возможных
- множество индексов, содержащее одну из возможных 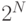 комбинаций первых
комбинаций первых  целых чисел,
целых чисел,  .
.
Модель нейрона Хебба
Структурная схема нейрона Хебба соответствует стандартной форме модели
нейрона (рис.1). Д.Хебб предложил формальное правило, в котором вес 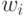 нейрона изменяется пропорционально произведению его входного
и выходного
сигналов
нейрона изменяется пропорционально произведению его входного
и выходного
сигналов
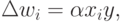
где  - коэффициент обучения.
- коэффициент обучения.
При обучении с учителем вместо выходного сигнала  используется
ожидаемая от этого нейрона реакция
используется
ожидаемая от этого нейрона реакция  . В этом случае правило Хебба
записывается в виде
. В этом случае правило Хебба
записывается в виде
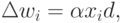
В каждом цикле обучения происходит суммирование текущего значения веса и
его приращения  :
:

В результате применения правила Хебба веса нейрона могут принимать
произвольно большие значения. Один из способов стабилизации процесса обучения
по правилу
Хебба состоит в учете последнего значения 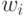 , уменьшенного на
коэффициент
забывания
, уменьшенного на
коэффициент
забывания  . При этом правило Хебба представляется в виде
. При этом правило Хебба представляется в виде

Значение  выбирается из интервала (0,1) и чаще всего
составляет
некоторый процент от коэффициента обучения
выбирается из интервала (0,1) и чаще всего
составляет
некоторый процент от коэффициента обучения  . Рекомендуемые
значения коэффициента
забывания -
. Рекомендуемые
значения коэффициента
забывания - 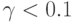 , при которых нейрон сохраняет
большую часть информации,
накопленной в процессе обучения, и получает возможность стабилизировать
значения весов на определенном уровне.
, при которых нейрон сохраняет
большую часть информации,
накопленной в процессе обучения, и получает возможность стабилизировать
значения весов на определенном уровне.
Стохастическая модель нейрона
В стохастической модели выходное состояние нейрона зависит не только от взвешенной суммы входных сигналов, но и от некоторой случайной переменной, значения которой выбираются при каждой реализации из интервала (0,1).
В стохастической модели нейрона выходной сигнал  принимает
значения
принимает
значения  с вероятностью
с вероятностью
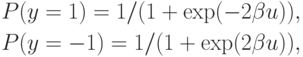
где  обозначает взвешенную сумму входных сигналов нейрона, а
обозначает взвешенную сумму входных сигналов нейрона, а  - положительная константа, которая чаще всего равна 1. Процесс обучения
нейрона в стохастической модели состоит из следующих этапов:
- положительная константа, которая чаще всего равна 1. Процесс обучения
нейрона в стохастической модели состоит из следующих этапов:
1) расчет взвешенной суммы
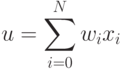
для каждого нейрона сети.
2) расчет вероятности  того, что
того, что  принимает
значение
принимает
значение  .
.
3) генерация значения случайной переменной  и
формирование
выходного
сигнала
и
формирование
выходного
сигнала  , если
, если 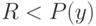 , или
, или 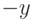 в
противном случае.
в
противном случае.
При обучении с учителем по правилу Видроу-Хоффа адаптация весов проводится по формуле