Радиальные нейронные сети
Многослойные нейронные сети, представленные в предыдущих разделах,
выполняют аппроксимацию функции нескольких переменных путем преобразования
множества входных переменных  в множество выходных
переменных
в множество выходных
переменных  .
Cигмоидальная функция активации по своему характеру осуществляет
аппроксимацию глобального типа. В результате ее нейрон, который был
однажды "включен" (после превышения суммарным сигналом
определенного
порогового значения), остается в этом состоянии при любом значении
сигнала, превышающем данный порог. Поэтому преобразование значения функции
в произвольной точке пространства выполняется объединенными усилиями
многих нейронов, что и объясняет название глобальная аппроксимация.
.
Cигмоидальная функция активации по своему характеру осуществляет
аппроксимацию глобального типа. В результате ее нейрон, который был
однажды "включен" (после превышения суммарным сигналом
определенного
порогового значения), остается в этом состоянии при любом значении
сигнала, превышающем данный порог. Поэтому преобразование значения функции
в произвольной точке пространства выполняется объединенными усилиями
многих нейронов, что и объясняет название глобальная аппроксимация.
Другой способ отображения входного множества в выходное заключается в преобразовании путем адаптации нескольких одиночных аппроксимирующих функций к ожидаемым значениям, причем эта адаптация проводится только в ограниченной области многомерного пространства. При таком подходе отображение всего множества данных представляет собой сумму локальных преобразований. С учетом роли, которую играют скрытые нейроны, преобразования составляют множество базисных функций локального типа. Выполнение одиночных функций (при ненулевых значениях) регистрируется только в ограниченной области пространства данных - отсюда и название локальная аппроксимация.
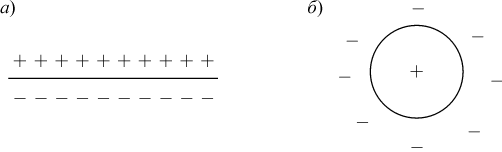
Рис. 1. Иллюстрация способов разделения пространства данных: а) сигмоидальным нейроном; б) радиальным нейроном
Особое семейство образуют сети с радиальной базисной функцией, в которых
нейроны реализуют функции, радиально изменяющиеся вокруг выбранного центра
и принимающие ненулевые значения только в окрестности этого центра.
Подобные функции, определяемые в виде 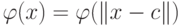 , будем называть
радиальными
базисными функциями. В таких сетях роль нейрона заключается в
отображении радиального пространства вокруг одиночной заданной точки
(центра) либо вокруг группы таких точек, образующих кластер. Суперпозиция
сигналов, поступающих от всех таких нейронов, которая выполняется выходным
нейроном, позволяет получить отображение всего многомерного пространства.
, будем называть
радиальными
базисными функциями. В таких сетях роль нейрона заключается в
отображении радиального пространства вокруг одиночной заданной точки
(центра) либо вокруг группы таких точек, образующих кластер. Суперпозиция
сигналов, поступающих от всех таких нейронов, которая выполняется выходным
нейроном, позволяет получить отображение всего многомерного пространства.
Сети радиального типа представляют собой естественное дополнение
сигмоидальных сетей. Сигмоидальный нейрон представляется в многомерном
пространстве гиперплоскостью, разделяющей это пространство на две
категории (два класса), в которых выполняется одно из двух условий: либо 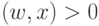 , либо
, либо  . Такой подход
продемонстрирован на рис. 1а.
. Такой подход
продемонстрирован на рис. 1а.
В свою очередь, радиальный нейрон представляет собой гиперсферу, которая
осуществляет шаровое разделение пространства вокруг центральной точки
(рис. 1б). Именно с этой точки зрения он является естественным дополнением
сигмоидального нейрона, поскольку в случае круговой симметрии данных
позволяет заметно уменьшить количество нейронов, необходимых для
разделения различных классов. Поскольку нейроны могут выполнять различные
функции, в радиальных сетях отсутствует необходимость использования
большого количества скрытых слоев. Структура типичной радиальной сети
включает входной слой, на который подаются сигналы, описываемые входным
вектором  , скрытый слой с нейронами радиального типа и выходной
слой,
состоящий, как правило, из одного или нескольких линейных нейронов.
Функция выходного нейрона сводится исключительно к взвешенному
суммированию сигналов, генерируемых скрытыми нейронами.
, скрытый слой с нейронами радиального типа и выходной
слой,
состоящий, как правило, из одного или нескольких линейных нейронов.
Функция выходного нейрона сводится исключительно к взвешенному
суммированию сигналов, генерируемых скрытыми нейронами.
