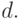Задача линейного разделения двух классов
Линейное разделение классов
состоит в построении линейного решающего правила,
т.е. такого вектора  , где
, где 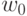 — порог, что при
— порог, что при  вектор
вектор  относится к первому классу, а при
относится к первому классу, а при 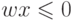 — ко второму.
— ко второму.
Разделение центров масс - простейший способ построения решающего правила. Суть этого способа заключается в вычислении вектора весов персептрона по следующей формуле
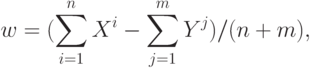
где 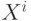 ,
, 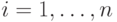 относятся к первому классу, а
относятся к первому классу, а 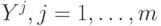 - ко второму.
- ко второму.
Линейные решающие правила, построенные на основании разделения центров масс, могут ошибаться на примерах из обучающей выборки даже в тех случаях, когда существует и безошибочное линейное разделение. Однако метод центров масс полезен как средство определения начального значения вектора весов для алгоритма обучения персептрона.
Алгоритм обучения персептрона по отдельным примерам
1. При изначально заданных значениях весов 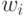 на вход
нейрона подается
обучающий вектор
на вход
нейрона подается
обучающий вектор  и рассчитывается значение выходного сигнала
и рассчитывается значение выходного сигнала 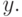 По результатам
сравнения
По результатам
сравнения  с
с  уточняются значения весов.
уточняются значения весов.
2. Если  , то
, то 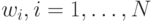 не
изменяются.
не
изменяются.
3. Если  , а
, а 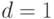 , то значения весов
уточняются по формуле
, то значения весов
уточняются по формуле
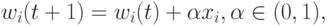
где  — коэффициент обучения,
— коэффициент обучения,  —
номер предыдущего цикла.
—
номер предыдущего цикла.
4. Если 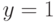 , а
, а 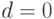 , то значения весов
уточняются по формуле
, то значения весов
уточняются по формуле
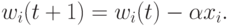
В обобщенной форме обучение персептрона на векторе  выражается формулой
выражается формулой
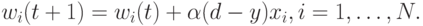
По завершении уточнения весовых коэффициентов представляются очередной
обучающий
вектор  и связанное с ним ожидаемое значение
и связанное с ним ожидаемое значение  , и
значения весов уточняются
заново. Этот процесс многократно повторяется на всей обучающей выборке, пока не
будут ликвидированы различия между всеми значениями
, и
значения весов уточняются
заново. Этот процесс многократно повторяется на всей обучающей выборке, пока не
будут ликвидированы различия между всеми значениями  и
соответствующими им
ожидаемыми значениями
и
соответствующими им
ожидаемыми значениями