Самоорганизация (самообучение) нейронных сетей
Классификация без учителя
Задан набор объектов, каждому объекту поставлен в соответствие вектор значений признаков (строка таблицы). Требуется разбить эти объекты на классы эквивалентности. Для каждого нового объекта нужно:
- Найти класс, к которому он принадлежит.
- Использовать новую информацию, полученную об этом объекте, для исправления (коррекции) правил классификации.
Отнесение объекта к классу проводится путем его сравнения с типичными элементами разных классов и выбора из них ближайшего.
Простейшая мера близости объектов - квадрат евклидова расстояния между векторами значений их признаков (чем меньше расстояние, тем ближе объекты). Соответствующее определение признаков типичного объекта - среднее арифметическое значение признаков по выборке, представляющей класс. Другая мера близости, возникающая при обработке сигналов, изображений и т.п. - квадрат коэффициента корреляции (чем он больше, тем ближе объекты). Возможны и иные варианты.
Если число классов  заранее определено, то задачу
классификации без
учителя можно поставить следующим образом.
заранее определено, то задачу
классификации без
учителя можно поставить следующим образом.
Метод динамических ядер в классификации без учителя
Пусть задана выборка предобработанных векторов данных 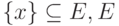 -
пространство векторов данных. Каждому классу будет соответствовать
некоторое ядро
-
пространство векторов данных. Каждому классу будет соответствовать
некоторое ядро 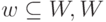 - пространство ядер.
- пространство ядер.
Для любых 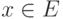 и
и 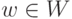 определим меру
близости
определим меру
близости 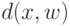 , а для каждого набора
из
, а для каждого набора
из  ядер
ядер  и любого разбиения
и любого разбиения  на
на  классов
классов 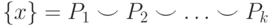 определим критерий качества
определим критерий качества
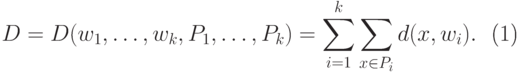 |
( 1) |
Требуется найти набор 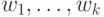 и разбиение
и разбиение 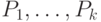 , минимизирующие
, минимизирующие 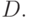 Шаг
алгоритма разбиваем на
Шаг
алгоритма разбиваем на  этапа:
этапа:
1) Для фиксированного набора ядер 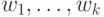 ищем
минимизирующее
ищем
минимизирующее  разбиение
разбиение 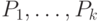 ; оно дается следующим решающим правилом:
; оно дается следующим решающим правилом: 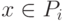 , если
, если 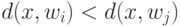 при
при 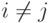 (когда для
(когда для  минимум
минимум 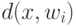 достигается
при
нескольких значениях
достигается
при
нескольких значениях  , выбор между ними может быть сделан
произвольно).
, выбор между ними может быть сделан
произвольно).
2) Для каждого 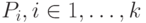 , полученного на первом
этапе, отыскивается
, полученного на первом
этапе, отыскивается 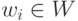 , минимизирующее критерий качества
, минимизирующее критерий качества
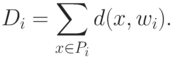
Начальные значения 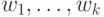 ,
, 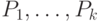 выбираются произвольно либо по
какому-нибудь эвристическому правилу. Если ядру
выбираются произвольно либо по
какому-нибудь эвристическому правилу. Если ядру 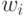 ставится в
соответствие элемент сети, вычисляющей по входному сигналу
ставится в
соответствие элемент сети, вычисляющей по входному сигналу  функцию
функцию 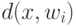 , то решающее правило для классификации дается
интерпретатором
"проигравший забирает все": элемент
, то решающее правило для классификации дается
интерпретатором
"проигравший забирает все": элемент  принадлежит
классу
принадлежит
классу  , если выходной
сигнал
, если выходной
сигнал  -го элемента
-го элемента 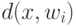 меньше всех остальных.
Мера близости
меньше всех остальных.
Мера близости  выбирается такой, чтобы легко можно было найти ядро
выбирается такой, чтобы легко можно было найти ядро 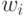 , минимизирущее
, минимизирущее 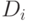 для данного
для данного