Модели нейронов

Сигмоидальный нейрон

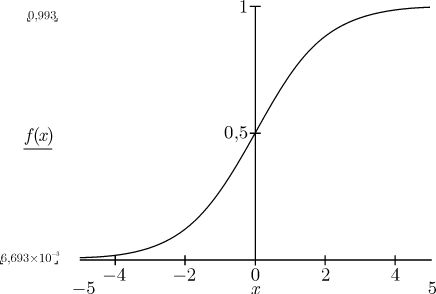
Нейрон сигмоидального типа имеет структуру, подобную модели МакКаллока-Питса, с той разницей, что функция активации является непрерывной и может быть выражена в виде сигмоидальной униполярной или биполярной функции. Униполярная функция, как правило, представляется формулой (рис.2)

,

Рис. 2. Униполярная функция

тогда как биполярная функция задается в виде (рис.3) .

Рис. 3. Биполярная функция

Параметр влияет на крутизну графика функции . При сигмоидальная функция превращается в функцию ступенчатого типа, идентичную функции активации персептрона. На практике чаще всего используется значение .

Важным свойством сигмоидальной функции является ее дифференцируемость. Для униполярной функции имеем

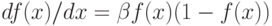
тогда как для биполярной функции

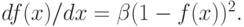
Применение непрерывной функции активации позволяет использовать при обучении градиентные методы оптимизации. Проще всего реализовать метод наискорейшего спуска, в соответствии с которым уточнение вектора весов проводится в направлении отрицательного градиента целевой функции , где

Компонента градиента имеет вид

где означает разницу между фактическим и ожидаемым значением выходного сигнала нейрона. Если ввести обозначение 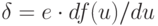, то можно получить выражение, определяющее -ю составляющую градиента в виде

Значения весовых коэффициентов уточняются по формуле

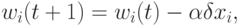
где .

Применение градиентного метода для обучения нейрона гарантирует достижение только локального минимума. Для выхода из окрестности локального минимума результативным может оказаться обучение с моментом. В этом методе процесс уточнения весов определяется не только информацией о градиенте функции, но и предыдущим изменением весов. Подобный способ может быть задан выражением

в котором первый член соответствует обычному методу наискорейшего спуска, тогда как второй член, называемый моментом, отражает последнее изменение весов и не зависит от фактического значения градиента. Значение выбирается из интервала (0,1).