Модели нейронов
Запись активации в замкнутой форме
Рассмотрим двухвходовый кубический модуль. Существует 4 значения активации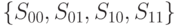 
. Выражение для активации будет
иметь
следующий вид:
- входной вектор. Такая запись вызвана тем, что
только
одно из произведений в сумме должно быть ненулевым. Для поляризованных
входов 
и 
активация
![\begin{align*}
u = [S_{00}(1-x_1)(1-x_2) + S_{01}(1-x_1)(1+x_2) +\\
+S_{10}(1+x_1)(1-x_2) + S_{11} (1+x_1)(1+x_2)]/4.
\end{align*}](/sites/default/files/tex_cache/110285f7dc1a0ec94da5beced733f7e8.png)
В случае 
- входового модуля получим
![\begin{align*}
u = [\sum_{\chi} S_\chi \prod_{i=1}^N (1+x_i)]/2^N.
\end{align*}](/sites/default/files/tex_cache/3a69b51f23abf90ad1f6d50f8ad367db.png)
Обучение кубических нейронов
Кубические нейроны обучаются путем изменения содержимого ячейки их памяти. Обозначим через `+' операцию инкремента-установки содержимого ячейки в +1, через `-' операцию декремента-установки в -1.
Пусть в начальном состоянии все ячейки кубического нейрона установлены в ноль. Обозначим ячейки, адресуемые обучающей выборкой, как центральные ячейки или центры. Ячейки, близкие к центрам в смысле расстояния Хемминга, будем настраивать на те же или близкие к ним значения, что и сами центры, т.е. должна происходить кластеризация значений ячейки вокруг центра. Это условие должно выполнятся для сети из кубических нейронов. Алгоритм обучения строит так называемое разбиение Вороного, при котором значение в ячейке определяется значением в ближайшем центре, а ячейки, равноудаленные от центров, остаются установленными в ноль. Кубические нейроны допускают большую функциональность, чем полулинейные, и поэтому, возможно, позволяют решать те же задачи при меньшем количестве модулей.