Модели нейронов
Аппроксимация функций
Нейрон типа "адалайн"
В нейроне типа "адалайн" (ADAptive LInear Neuron - адаптивный линейный нейрон) адаптивный подбор весовых коэффициентов осуществляется в процессе минимизации квадратичной ошибки, определяемой как
![E(w)=e^{2}/2 =[d-(\sum_{i=0}^{N} w_{i} x_{i})]^{2}/2.](/sites/default/files/tex_cache/7ba4d13fdb401f9161ee0672d491cf9e.png)
В связи с выполнением условия дифференцируемости целевой функции стало возможным применение алгоритма градиентного обучения. Значения весовых коэффициентов уточняются следующим способом
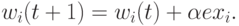
Паде-нейрон
Паде-нейрон вычисляет произвольную дробно-линейную функцию вектора  .
Так же, как и для адаптивного сумматора, числитель и знаменатель можно
сделать линейными функциями
.
Так же, как и для адаптивного сумматора, числитель и знаменатель можно
сделать линейными функциями  :
:
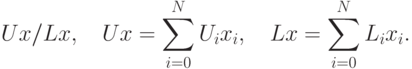
Паде-нейрон может использоваться как обобщение нейрона типа "адалайн" в тех случаях, когда линейных функций становится недостаточно, в частности, в задачах интерполяции эмпирических зависимостей.
В случае Паде-нейрона квадратичная ошибка определяется как
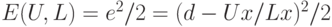
и значения весовых коэффициентов уточняются по следующим формулам

Нейрон с квадратичным сумматором
Квадратичный сумматор может вычислять произвольный полином второго порядка от вектора входных сигналов
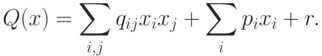
Для многомерных нормальных распределений нейрон с квадратичным сумматором является наилучшим классификатором. Минимум вероятности ошибки дает квадратичная разделяющая поверхность:
если  , то объект принадлежит первому классу;
, то объект принадлежит первому классу;
если 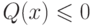 , то объект принадлежит второму классу (при
условии
правильного выбора коэффициентов Q(x)).
, то объект принадлежит второму классу (при
условии
правильного выбора коэффициентов Q(x)).
Квадратичная ошибка здесь определяется как

Коэффициенты квадратичного сумматора уточняются по формулам
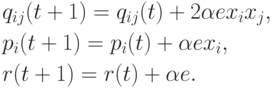
Недостаток такого классификатора - большое число настраиваемых параметров.
