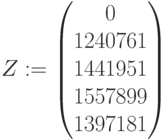Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Лекция 2:

Финансово-экономические модели
A
|
версия для печати
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

2.5. Элементы анализа инвестиционных проектов

Инвестиционный проект – комплекс действий (работ, услуг, управленческих операций и решений), направленных для осуществления действий, связанных с размещением капитала. Исходное условие инвестирования капитала – получение в будущем прибылей, которые возмещают инвестированные затраты капитала. Для принятия инвестиционных решений необходим экономический подход, учитывающий изменение ценности денег во времени. В основу анализа инвестиционных проектов положен инструмент финансовой математики – дисконтирование денежного потока. Рассмотренные выше финансовые показатели нерегулярного денежного потока являются базовыми показателями инвестиционного проекта. Кроме этого, водятся чисто экономические показатели

Денежный поток проекта — это зависимость от времени денежных поступлений и затрат, порожденных инвестиционным проектом, на протяжении всего периода его реализации.

Финансовыми показателями проекта являются

  • чистая текущая стоимость npv;
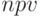  • внутренняя норма доходности irr;
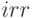  • срок окупаемости простого потока без учета дисконтирования pbp;
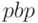  • срок окупаемости инвестиций с учетом дисконтирования dpbp;
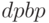  • индекс рентабельности инвестиций PI/

При анализе проекта 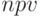npv удобно записывать в виде:

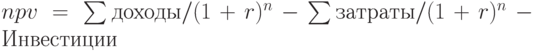npv=\sum_{}^{}доходы/(1+r)^n-\sum_{}^{}затраты/(1+r)^n-Инвестиции где r – ставка дисконтирования.

В качестве ставки дисконтирования в большинстве случаев выбирается величина средневзвешенной стоимости капитала и может быть скорректирована на показатели возможного риска, связанного с реализацией конкретного проекта и ожидаемого уровня инфляции. В качестве ставки дисконтирования можно выбрать доходность ценных бумаг с риском, аналогичным риску инвестиционного проекта. Иногда в качестве дисконтной ставки используется величина ставки рефинансирования.

Примеры решения задач

Задача 2.8.

Предприятие инвестирует в модернизацию сумму в размере 500000 тыс. руб. Рассматривается проект в течение 1 года. Денежные потоки от операционной деятельности по кварталам в течение года представлены в таблице 2.3. Определить финансовые показатели проекта: чистую дисконтированную стоимость 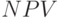NPV, внутреннюю доходность проекта, индекс рентабельности, времена окупаемости. Построить финансовый профиль проекта. Провести анализ для разных ставок дисконтирования.

Таблица 2.3.
Кварталы Выручка (тыс.руб) Затраты (тыс.руб) Налоги и сборы (тыс.руб) Инвестиции (тыс.руб) Чистый денежный поток(тыс.руб)
0 -500000 -500000
1 1388000 1240761 22086 125153
2 1642000 1441951 30007 170042
3 1833650 1557899 41363 234388
4 1568000 1397181 25623 145196

Решение.

Представлено на рисунках 2.10, 2.11, 2.12. Для решения используем методику оценки денежного потока, приведенную в примере 2.7. Данные вводятся также в виде векторов. Дисконтированные стоимости и чистые дисконтированные стоимости рассчитываются в виде матриц. Инвестиционный анализ проведен для 5 ставок дисконтирования. Годовые ставки дисконтирования выбраны в диапазоне от 0 до 60%, вектор 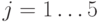r_j j=1…5. Поскольку денежные суммы поступают по кварталам, при расчетах используется периодическая ставка, равная 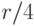r/4. Найденная внутренняя доходность проекта 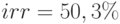irr=50,3\%. Поэтому чистая дисконтированная стоимость положительна - 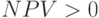NPV>0 для ставок дисконтирования до 50%, для ставки дисконтирования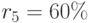 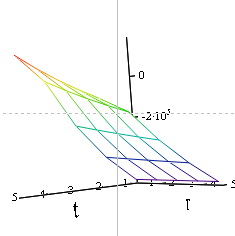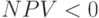r_5 =60\% NPV<0. Это демонстрирует финансовый профиль проекта. Индекс рентабельности 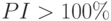PI>100\% для ставок 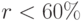r<60\%. Проект окупается до ставок 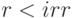r< irr . Времена окупаемости определены.

Определение финансовых параметров инвестиционного проекта

ORIGIN:=1

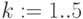
Время поступления (кварталы): 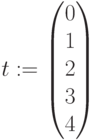t:=\begin{pmatrix} 0 \\ 1\\ 2\\ 3\\ 4 \end{pmatrix}, k:=1..5

Выручка: P:=\begin{pmatrix} 0 \\ 1388000\\ 1642000\\ 1833650\\ 1568000 \end{pmatrix}

Затраты: Z:=\begin{pmatrix} 0 \\ 1240761\\ 1441951\\ 1557899\\ 1397181\end{pmatrix}

Налоги и сборы: 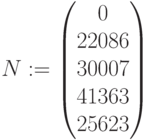N:=\begin{pmatrix} 0 \\ 22086\\ 30007\\ 41363\\ 25623\end{pmatrix}

Инвестиции: 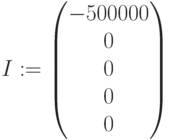I:=\begin{pmatrix} -500000 \\ 0\\ 0\\ 0\\ 0\end{pmatrix}

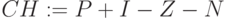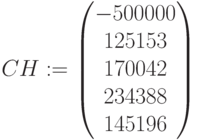
Чистые поступления с инвестиций: CH:=P+I-Z-N, CH:=\begin{pmatrix} -500000 \\ 125153\\ 170042\\ 234388\\ 145196\end{pmatrix}

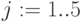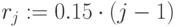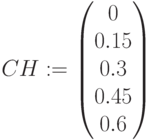
Ставки дисконтирования: j:=1..5, r_j:=0.15\cdot(j-1), CH:=\begin{pmatrix} 0\\ 0.15\\ 0.3\\ 0.45\\ 0.6\end{pmatrix}

Дисконтированные стоимости и чистые приведенные стоимости проекта

Рис. 2.10. Дисконтированные стоимости и чистые приведенные стоимости проекта

Решение:

Дисконтированные стоимости 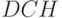DCH для 5 ставок по кварталам

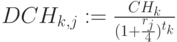
DCH_{k,j}:=\frac{CH_k}{(1+\frac{r_j}{4})^{t_k}}

DCH:=\begin{array}{|c|c|c|c|c|c|} \hline & 1 & 2 & 3 & 4 & 5 \\ \hline 1& -5\cdot 10^5 & -5\cdot 10^5 & -5\cdot 10^5 & -5\cdot 10^5 & -5\cdot 10^5 \\ \hline2& 1\cdot 10^5 & 1\cdot 10^5 & 1\cdot 10^5 & 1\cdot 10^5 & 1\cdot 10^5 \\ \hline3& 2\cdot 10^5 & 2\cdot 10^5 & 1\cdot 10^5 & 1\cdot 10^5 & 1\cdot 10^5 \\ \hline4& 2\cdot 10^5 & 2\cdot 10^5 & 2\cdot 10^5 & 2\cdot 10^5 & 2\cdot 10^5 \\ \hline5& 1\cdot 10^5 & 1\cdot 10^5 & 2\cdot 10^5 & 9\cdot 10^4 & 8\cdot 10^4 \\ \hline \end{array}

Чистая дисконтированная стоимость 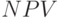NPV для 5 ставок

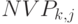NVP_{k,j}:=(\sum_{i=1}^{k}DCH_{i,j})

NVP_{k,j} – чистая приведенная стоимость для момента времени t_k и ставки дисконтирования r_j

NVP:=\begin{array}{|c|c|c|c|c|c|} \hline & 1 & 2 & 3 & 4 & 5 \\ \hline 1& -500000 & -500000 & -500000 & -500000 & -500000 \\ \hline2& -374847 & -379371 & -383579 & -387503 & -391171 \\ \hline3& -204805 & -211399 & -236436 & -250113 & 262595 \\ \hline4& 29583 & -11519 & -47763 & -79883 & -108481 \\ \hline5& 174779 & 113796 & 60960 & 14905 & -25465 \\ \hline \end{array}

Определение внутренней доходности

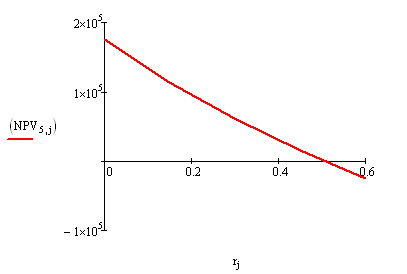
График чистой приведенной стоимости 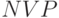NVP всего потока от ставки дисконтирования. Точка пересечения – внутренняя доходность.

Внутренняя доходность проекта

Рис. 2.11. Внутренняя доходность проекта
Дальше >>
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Вопросы и ответы

вопросов: 0