НОУ ИНТУИТ | Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования. Лекция 2: Финансово-экономические модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Уральский государственный экономический университет

Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 471 / 50 | Длительность: 11:44:00

Темы: Математика, Экономика, Образование

|

Вам нравится? Нравится 25 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Задача 2.4.

Проанализировать, сколько лет предприятие будет расплачиваться с кредитом в размере 90 млн.руб, при разных вариантах ежегодных выплат: 30 млн.руб., 60 млн.руб, 80 млн.руб. Выплаты поступают в конце года. Рассматриваются процентные ставки 10%, 12%,15%, 20%,25%. Проценты начисляются раз в год. Каковы суммарные выплаты предприятия для каждого варианта ставки и ежегодного платежа.

Решение. (рис. 2.4)

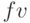Данные вводятся в виде векторов: pmt и . Для расчета срока оплаты кредита $n_{ij}$ для разных выплат pmt_i и ставки r_j используем формулу (2.24). Из финансовых функций выбираем nper (rate,pmt, pv, [[fv], [type]) , которая находит число периодов для вклада (займа) pv, периодичных постоянных платежей pmt , использующих фиксированную процентную ставку rate ; - остаток долга, [type] – тип ренты. В квадратных скобках необязательные аргументы. Финансовая функция nper() при расчетах учитывает движение денег: если платежи вносятся – отрицательные, то 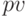сумма кредита получена - величина положительная.

Расчет срока погашения кредита.

Входные данные: Обозначим pmt – платеж, – номер ставки, – номер платежа

pv:=90 , $pmt:=\begin{pmatrix} 30 \\ 60 \\ 80 \end{pmatrix}$ , $r:=\begin{pmatrix} 10\% \\ 12\% \\ 15\% \\ 20\% \\ 25\% \end{pmatrix}$

ORIGIN:=1 , i:=1..3 , j:=1..5

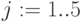
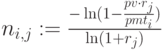
$n_{i,j}:=\frac{-\ln(1-\frac{pv\cdot r_j}{pmt_i})}{\ln(1+r_j)}$

$r^T=\begin{pmatrix} 0.1 & 0.12 & 0.15 & 0.2 & 0.25 \end{pmatrix}$

$n=\begin{pmatrix} 3.7 & 3.9 & 4.3 & 5 & 6.2 \\ 1.7 & 1.8 & 1.8 & 2 & 2.1 \\ 1.3 & 1.3 & 1.3 & 1.4 & 1.5 \end{pmatrix}$ , $pmt=\begin{pmatrix} 30\\ 60 \\ 80 \end{pmatrix}$

Используем встроенную финансовую функцию nper(rate,pmt,pv,[fv],[type])

$nf_{i,j}:=nper[r_j,(-pmt),pv,0,0]$

$nf=\begin{pmatrix} 3.7 & 3.9 & 4.3 & 5 & 6.2 \\ 1.7 & 1.8 & 1.8 & 2 & 2.1 \\ 1.3 & 1.3 & 1.3 & 1.4 & 1.5 \end{pmatrix}$

Суммарные выплаты для серии ставок и ежегодных платежей

$S_{i,j}:=n_{i,j}\cdot pmt_i$

$r^T=\begin{pmatrix} 0.1 & 0.12 & 0.15 & 0.2 & 0.25 \end{pmatrix}$

$S=\begin{pmatrix} 112 & 118 & 128 & 151 & 186 \\ 102 & 105 & 109 & 117 & 126 \\ 100 & 102 & 106 & 112 & 118 \end{pmatrix}$ , $pmt=\begin{pmatrix} 30\\ 60 \\ 80 \end{pmatrix}$

Рис. 2.4. Графики

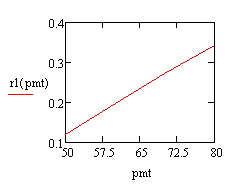
Построим график: срок выплаты от ставки и по годам

$W(r,pmt):=\frac{-\ln(1-\frac{pv\cdot r}{pmt_i})}{\ln(1+r)}$

M=CreateMesh(W,0.1,0.25,30,60)

Задача 2.5.

Рассчитать годовую процентную ставку для кредита 180 млн.руб., выданного на срок 5 лет. Оплата кредита производится постоянными ежегодными выплатами. Проанализировать варианты ежегодных выплат: 50 млн.руб., 60 млн.руб., 70 млн.руб., 80 млн.руб.

Решение. (рис.2.5)

Для расчета ставки используем формулу (2.23). Платеж pmt представляем в виде ранжированной переменной. Строим функцию

$f(pmt,r)=pmt-\frac{pv\cdot r}{[1-(1+r)^{-n}]}$ ,

( 2.27)

и решаем уравнение численно относительно , используя функцию root() для разных платежей.

Из финансовых функций выбираем rate(nper,pmt,pv,[fv],[type],[guess] ) , где guess — начальное значение корня для аппроксимации. Пусть $guess=0.1(10\%)$ .

Входные данные

Обозначим 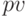– сумма кредита, pmt – платежи, –срок, – ставка

pv:=180 , n:=5 , m:=1 , pmt:=50, 60..80

Решение:

$f(pmt,r):=[pmt-\frac{pv\cdot r}{[1-(1+r)^{-n}]}]$

r:=0.11

r1(pmt):=root(f(r,pmt),r)

$r1(pmt):=\begin{array}{|c|} \hline 0.12 \\ \hline 0.2 \\ \hline 0.27 \\ \hline 0.34 \\ \hline \end{array}$

Рис. 2.5. График процентной ставки от платежа

Применим финансовую функцию

pmt:=50, 60..80

rf(pmt):=rate(n,-pmt,pv,0,0,0.1)

$rf(pmt):=\begin{array}{|c|} \hline 0.12 \\ \hline 0.2 \\ \hline 0.27 \\ \hline 0.34 \\ \hline \end{array}$

Задача 2.6.

Банк планирует ежегодно получать гарантированные денежные поступления в размере 23 млн.руб. в течение 5 лет. Какой кредит должен предоставить банк при годовой процентной ставке 15%, 20%, 22% ?

Решение. (рис.2.6)

Здесь используем формулу (2.22) и альтернативно финансовую функцию pv (rate,nper, pmt, [fv], [type]) , которая находит текущее значение заема, основанное на периодичности и постоянных платежах pmt , через данное число составных периодов nper , использующее фиксированную процентную ставку rate, [type] – тип ренты. Данные и функции представляем в виде матриц. Поскольку платежи поступают в банк pmt>0 , финансовая функция рассчитает суммы кредита отрицательные.

Входные данные

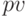Обозначим pmt – ежегодные денежное поступление, – годы, – процентная ставка, – кредит

$pmt:=10\cdot 10^6$

$n:=\begin{pmatrix} 1 \\ 2 \\ 3 \\ 5 \end{pmatrix}$

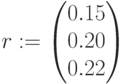
$r:=\begin{pmatrix} 0.15 \\ 0.20 \\ 0.22 \end{pmatrix}$

Решение:

ORIGIN:=1 , i:=1..3 , j:=1..4

$pv1_{i,j}:=pmt\cdot \frac{[1-(1+r_i)^{-n_j}]}{r_i}$

$pv1=\begin{pmatrix} 8.696\times 10^6 & 1.626\times 10^7 & 2.283\times 10^7 & 3.352\times 10^7 \\ 8.333\times 10^6 & 1.528\times 10^7 & 2.106\times 10^7 & 2.991\times 10^7 \\ 8.197\times 10^6 & 1.492\times 10^7 & 2.042\times 10^7 & 2.864\times 10^7 \end{pmatrix}$

Используем для рассчета финансовую функцию

$pvf_{i,j}:=pv(r_i,n_j,pmt)$

$pvf=\begin{pmatrix} -8.696\times 10^6 & -1.626\times 10^7 & -2.283\times 10^7 & -3.352\times 10^7 \\ -8.333\times 10^6 & -1.528\times 10^7 & -2.106\times 10^7 & -2.991\times 10^7 \\ -8.197\times 10^6 & -1.492\times 10^7 & -2.042\times 10^7 & -2.864\times 10^7 \end{pmatrix}$

Построим диаграмму: Размер кредита от ставки по годам

Рис. 2.6. Размер кредита от ставки по годам

Дальше >>

Авторизоваться

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Финансово-экономические модели

Вопросы и ответы