Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Уральский государственный экономический университет
Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 467 / 49 | Длительность: 11:44:00
Темы: Математика, Экономика, Образование
Лекция 2:

Финансово-экономические модели
A
|
версия для печати
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

2.4. Нерегулярный денежный поток

Рассмотрим нерегулярный денежный поток – поток неравных платежей 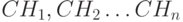CH_1, CH_2 …CH_n , совершаемых через неравные промежутки времени [1,3]. Процентная ставка r – постоянна, n – число периодов, платежи 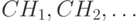CH_1, CH_2, … различаются по величине и знаку. Положительные 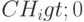CH_i&gt;0 – доходы, отрицательные 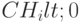CH_i &lt;0 – вложения (затраты).

Чистая дисконтированная стоимость

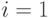Для оценки текущей стоимости используется дисконтирование денежных потоков – приведение их разновременных значений к стоимости на определенный момент времени, который называется моментом приведения [8,13,14] . Используется ставка дисконтирования r, которая отражает стоимость денег с учетом временного фактора. Результат приведения нерегулярного потока к моменту i=1 поступлений - дисконтированная стоимость потока равная сумме дисконтированных поступлений - DCH_i имеет вид:

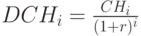DCH_i=\frac{CH_i}{(1+r)^i} ( 2.28)

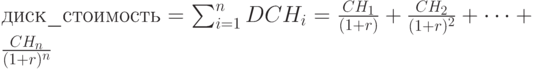диск\_стоимость=\sum_{i=1}^{n}DCH_i=\frac{CH_1}{(1+r)}+ \frac{CH_2}{(1+r)^2}+…+\frac{CH_n}{(1+r)^n} ( 2.29)

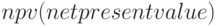Пусть в начальный момент i=0 вложена сумма денег - начальная инвестиция I , она отрицательна. Для оценки эффективности финансовой операции вложения вводится показатель - чистая современная стоимость npv (net present value) (или чистая дисконтированная стоимость, или чистый дисконтированный доход):

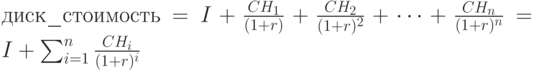диск\_стоимость=I+\frac{CH_1}{(1+r)}+ \frac{CH_2}{(1+r)^2}+…+\frac{CH_n}{(1+r)^n}=I+\sum_{i=1}^{n}\frac{CH_i}{(1+r)^i} ( 2.30)

Чистая дисконтированная стоимость показывает, насколько современная стоимость текущих платежей (доходов и вложений) превышает инвестиционные затраты I в начальный момент времени.

Индекс рентабельности инвестиций PI (Profitability Index)

Отношение дисконтированного денежного потока к первоначальным инвестициям:

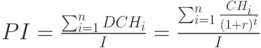PI=\frac{\sum_{i=1}^{n}DCH_i}{I}=\frac{\sum_{i=1}^{n}\frac{CH_i}{(1+r)^i}}{I} ( 2.31)

Показатель 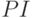PI также оценивает эффективность вложения инвестиций. Если дисконтированная стоимость превышает инвестиционные затраты I в начальный момент времени то PI&gt;1.

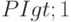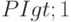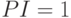Таким образом, PI&gt;1 — вложение инвестиций выгодно, PI &lt; 1 — вложение инвестиций невыгодно, PI = 1 — ни прибыли, ни убытков.

Внутренняя норма доходности

Представляет интерес определение ставки r, при которой все дисконтированные положительные выплаты (доходы), начальная инвестиция I и дисконтированные отрицательные выплаты (затраты) уравниваются [13,14]. Такое значение r называется внутренней нормой доходности – 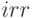irr (internal rate of return). Значение 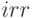irr определяется решением уравнения npv=0 относительно r:

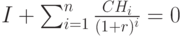I+\sum_{i=1}^{n}\frac{CH_i}{(1+r)^i}=0 ( 2.32)

Внутренняя норма доходности имеет смысл нормы дохода на инвестицию, если имеется одно поступление денег. Действительно, если начальная инвестиция 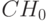CH_0, поступает один платеж 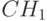CH_1 , имеем

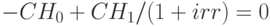-CH_0+CH_1/(1+irr)=0,

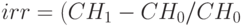irr=(CH_1-CH_0/CH_0 ( 2.33)

Таким образом, чистая дисконтированная стоимость показывает, достигнут ли инвестиции за экономический срок их жизни желаемого уровня отдачи. Различные варианты:

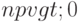  1. npv &gt;0 вложение инвестиций выгодно,
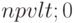  2. npv &lt;0 вложение инвестиций невыгодно, вложенные средства превышают доход,
  3. npv =0 эффект от инвестиций нулевой.

Срок окупаемости

Параметр, определяющий временную характеристику потока - срок окупаемости - минимальный временной период, за который инвестиция и доходы перекрывают все расходы [13,14]. Момент окупаемости - наиболее ранний момент времени в расчетном периоде, в который кумулятивные (накопленные) денежные поступления обращаются в нуль и в дальнейшем остаются неотрицательными. Различают срок окупаемости простого потока (рассчитываются простые поступления) 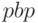pbp (Pay-Back Period) и дисконтированного потока (рассчитываются дисконтированные поступления) – 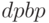dpbp (Discounted Pay-Back Period). Срок окупаемости определяется по следующим уравнениям:

  • для простого потока pbp:
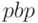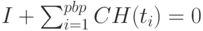
    I+{\sum_{i=1}^{pbp}CH(t_i)=0 ( 2.34)
  • для дисконтированного потока срок окупаемости dpbp:
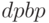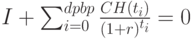
    I+{\sum_{i=0}^{dpbp}\frac{CH(t_i)}{(1+r)^{t_i}}=0 ( 2.35)

Срок окупаемости рассчитывается в периодах, в которые поступают платежи. Затем можно пересчитать для любых единиц (годы, кварталы и т.д.).

Рассмотрим этапы расчета срока окупаемости.

Пусть платежи поступают по годам.

Схема расчета срока окупаемости pbp для простого потока.

  1. Рассчитать кумулятивные денежные потоки (накопленную сумму всех платежей последовательно на каждый год ).
  2. Определить момент (год) получения первой положительной величины – окупаемость произошла между этим годом и предыдущим.
  3. Определить срок окупаемости с долей года по формуле: pbp=(год\_окупаемости-1)+\frac{наколенная\_стоимость\_за\_предшествующий\_год}{платеж\_в\_год\_окупаемости}

Схема расчета срока окупаемости dpbp для дисконтированного потока.

  1. Рассчитать дисконтированный денежный поток платежей, исходя из ставки дисконта r и начала потока.
  2. Повторить этапы 1-3 схемы расчета для простого потока применительно к дисконтированному потоку.
dpbp=(год\_окупаемости-1)+\frac{дисконтированная\_наколенная\_стоимость\_за\_предшествующий\_год}{дисконтированный\_платеж\_в\_год\_окупаемости}

Пример 2.1

Вложена начальная инвестиция 10 млн. руб. В первый год вкладывается еще 1 млн.руб. Предполагаемые денежные доходы в последующие три года: 3 млн, 5 млн, 8 млн. руб. Рассчитать срок окупаемости простого и дисконтированного потока, для ставки дисконтирования 10%.

Таблица 2.1.
Период Денежные поступления (млн.руб.) Накопленный денежный поток Дисконтированные поступления по ставке 10% Накопленный дисконтированный денежный поток
0 -11 -11 -11 -11
1 -1 -12 -0,91 -11,91
2 8 -4 6,61 -5,30
3 5 1 3,76 -1,54
4 8 9 5,46 3,92

Срок окупаемости простого потока.

Простой поток на 2 год еще не окупился (накопленный поток = - 4), но за счет поступления 5 млн. за 3 год уже окупился. Срок окупаемости 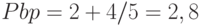Pbp =2+4/5=2,8 года.

Срок окупаемости дисконтированного потока.

Дисконтированный поток на 3 год еще не окупился (накопленный поток = - 1,54 млн), но за счет поступления 5,46 млн. за 4 год уже окупился. Срок окупаемости 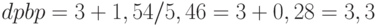dpbp =3+1,54/5,46=3+0,28 =3,3 года.

Дальше >>
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Вопросы и ответы

вопросов: 0