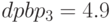Финансово-экономические модели
Примеры решения задач
Задача 2.7.
Имеется поток денежных платежей разной величины и знака. Срок денежного потока 6 лет. В начале срока вложена сумма 850 тыс. руб. В первый и второй год предполагается вложить еще 250 и 100 тыс. руб., соответственно. Предполагаемые дальнейшие денежные поступления: 550, 700, 500 и 220 тыс.руб. (см. таблицу 2.2). Определить финансовые параметры денежного потока: чистую современную стоимость 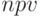 , внутреннюю норму доходности
, внутреннюю норму доходности 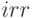 , сроки окупаемости:
, сроки окупаемости: 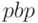 для простого потока и
для простого потока и 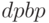 для дисконтированного потока. Построить финансовый профиль денежного потока и график
для дисконтированного потока. Построить финансовый профиль денежного потока и график 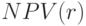 , демонстрирующий внутреннюю доходность.
, демонстрирующий внутреннюю доходность.
Решение.
Приведено на рисунках 2.7, 2.8 и 2.9. Здесь используем уравнения (2.28), (2.30), (2.32), (2.34), (2.35). Данные вводим в виде векторов: годы поступлений 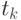 , в момент
, в момент 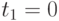 поступает инвестиция
поступает инвестиция 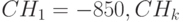 – поступления для
– поступления для 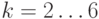 . Для расчета дисконтированной стоимости, надо выбрать ставку дисконтирования r. Выбор ставки дисконтирования определяется многими факторами: экономической конъюнктурой, типом осуществляемых инвестиций, степенью риска. Расчет проведен для 6 ставок в диапазоне от 0 до 30%, вектор
. Для расчета дисконтированной стоимости, надо выбрать ставку дисконтирования r. Выбор ставки дисконтирования определяется многими факторами: экономической конъюнктурой, типом осуществляемых инвестиций, степенью риска. Расчет проведен для 6 ставок в диапазоне от 0 до 30%, вектор 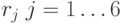 – ставки дисконтирования. Дисконтированные платежи
– ставки дисконтирования. Дисконтированные платежи  и чистая дисконтированная стоимость
и чистая дисконтированная стоимость  для моментов времени
для моментов времени  и ставок
и ставок 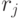 рассчитаны в виде матриц. Найдена внутренняя доходность
рассчитаны в виде матриц. Найдена внутренняя доходность 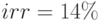 . Для ставок дисконтирования , больших внутренней доходности
. Для ставок дисконтирования , больших внутренней доходности 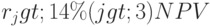 отрицательна. Построен финансовый профиль - графическое представление чистых кумулятивных денежных поступлений и чистой дисконтированной стоимости с нарастающим итогом для
отрицательна. Построен финансовый профиль - графическое представление чистых кумулятивных денежных поступлений и чистой дисконтированной стоимости с нарастающим итогом для  при норме дисконта
при норме дисконта  . Рассчитаны времена окупаемости для простого потока pbp=3.9 года и дисконтированного потока для
. Рассчитаны времена окупаемости для простого потока pbp=3.9 года и дисконтированного потока для 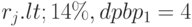 , года (
, года ( дисконтирования 5%= ) и
дисконтирования 5%= ) и 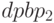 =4,9 года (
=4,9 года ( дисконтирования =10% ) . Денежный поток окупается до конечного срока. Для ставок, больших внутренней доходности
дисконтирования =10% ) . Денежный поток окупается до конечного срока. Для ставок, больших внутренней доходности 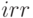 , денежный поток не окупается.
, денежный поток не окупается.
Финансовые параметры денежного потока неравных платежей

Платежи и инвестиции: 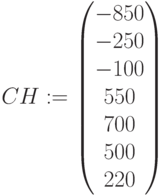
Время поступления (годы): 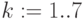 ,
, 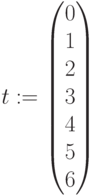
Ставки дисконтирования: 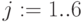 ,
, 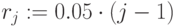 ,
, 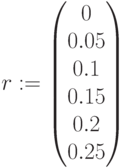
Решение:
Дисконтированные стоимости платежей 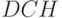 для 6 ставок
для 6 ставок

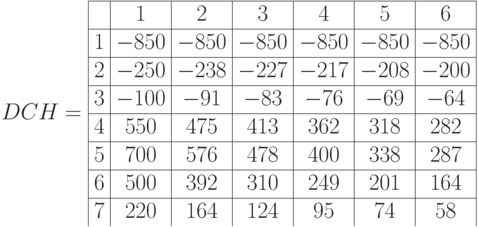
Чистая дисконтированная стоимость 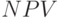 для 6 ставок
для 6 ставок
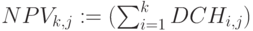
 - чистая приведенная стоимость для момента времени
- чистая приведенная стоимость для момента времени  и ставки дисконтирования
и ставки дисконтирования 

Определение внутренней доходности
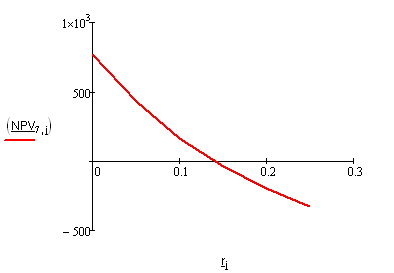
График чистой приведенной стоимости 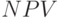 всего потока от ставки. Точка пересечения – внутренняя доходность.
всего потока от ставки. Точка пересечения – внутренняя доходность.
Для определения внутренней доходности используем финансовую функцию 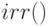 :
: 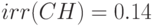
Внутренняя доходность 14%.
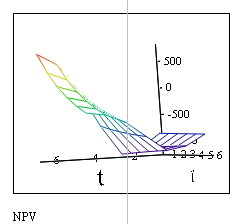
График поступлений и 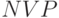 от времени – финансовый профиль для разных ставок дисконтирования
от времени – финансовый профиль для разных ставок дисконтирования
Кумулятивный простой поток поступлений – чистые поступления
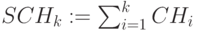
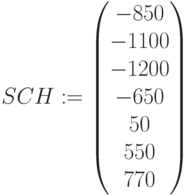 ,
, 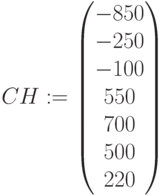

NVP от времени для разных ставок дисконтирования – 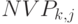 – кумулятивный дисконтированный поток или NVP с нарастающим итогом по годам
– кумулятивный дисконтированный поток или NVP с нарастающим итогом по годам  для ставки дисконтирвования
для ставки дисконтирвования 

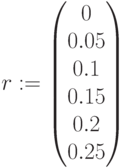
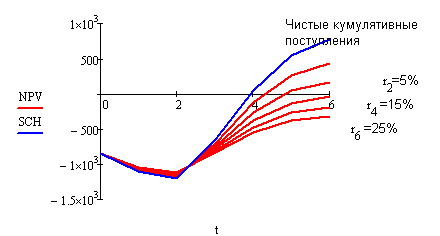
Рис. 2.9. Кумулятивные поступления и чистая дисконтированная стоимость от времени для ряда ставок дисконтирования
Определение индекса прибыльности и сроков окупаемости простого и дисконтированного потока.
Индекс рентабельности для разных ставок дисконтирования
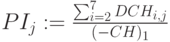
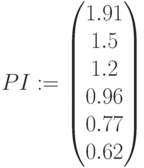
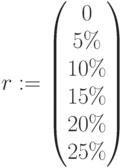
PI в процентах:
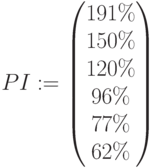
Определение срока окупаемости (годы). Срок окупаемости pbp для простого потока:
Кумулятивный простой поток  в 3 год
в 3 год  и меняет знак на 4 год = 50 засчет поступления
и меняет знак на 4 год = 50 засчет поступления 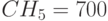 (тыс).
(тыс).
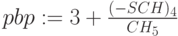 ,
, 
Сроки окупаемости dpbp дисконтированного поток адля разных ставок дисконтирования. Используем дисконтированные стоимости постулений 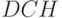 .
.
Для ставок дисконтирования 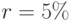 (
( ) и
) и 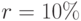 (
( ) NPV меняет знак на 5 год.
) NPV меняет знак на 5 год.
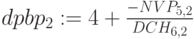
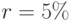 ,
, 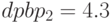
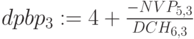
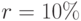 ,
,