Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Уральский государственный экономический университет
Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 467 / 49 | Длительность: 11:44:00
Темы: Математика, Экономика, Образование
Лекция 2:

Финансово-экономические модели
A
|
версия для печати
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Для определения внутренней доходности использует финансовую функцию 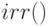irr(). Учитыываем, что поступления идут по кварталам.

irr(CH)\cdot 4=0.503. Внутренняя доходность 50,3%.

График поступлений и 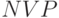NVP от времени – финансовый профиль для разных ставок дисконтирования

Кумулятивный простой поток постулений – чистые поступления:

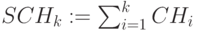SCH_k:=\sum_{i=1}^{k}CH_i, SCH_k:=NVP_{k,1}

SCH:=\begin{pmatrix} -500000 \\ -374847 \\ -204805\\ -29583\\ 174779\end{pmatrix}, CH:=\begin{pmatrix} -500000 \\ 125153\\ 170042\\ 234388 \\ 145196\end{pmatrix}

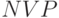NVP от времения для разных ставок дисконтирования – 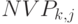NVP_{k,j} – кумулятивный дисконтированный поток или 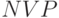NVP с нарастающим итогом

NVP:=\begin{array}{|c|c|c|c|c|c|} \hline & 1 & 2 & 3 & 4 & 5 \\ \hline 1& -500000 & -500000 & -500000 & -500000 & -500000 \\ \hline2& -374847 & -379371 & -383579 & -387503 & -391171 \\ \hline3& -204805 & -211399 & -236436 & -250113 & 262595 \\ \hline4& 29583 & -11519 & -47763 & -79883 & -108481 \\ \hline5& 174779 & 113796 & 60960 & 14905 & -25465 \\ \hline \end{array}

r:=\begin{pmatrix} 0 \\ 0.15\\ 0.3\\ 0.45\\ 0.6\end{pmatrix}

Финансовый профиль проекта

Рис. 2.12. Финансовый профиль проекта

Индекс рентабельности для разных ставок дисконтирования

PI_j:=\frac{\sum_{i=2}^{5}DCH_{i,j}}{(-CH)_I}, PI:=\begin{pmatrix} 1.35 \\ 1.23\\ 1.12\\ 1.03\\ 0.95\end{pmatrix}, r:=\begin{pmatrix} 0\% \\ 15\%\\ 30\%\\ 45\%\\ 60\%\end{pmatrix}

PI в процентах: PI:=\begin{pmatrix} 135\% \\ 123\%\\ 112\%\\ 103\%\\ 95\%\end{pmatrix}

Определение срока окупаемости (кварталы, месяцы):

Для простого потока pbp:

Кумулятивный простой поток SCH в 3 квартал меняет знак на 4 год = 50 засчет поступлений 234388.

pbp:=2+\frac{(-SCH)_3}{CH_4}, pbp=2.9, pbp\cdot 3=8.6

Для дисконтированного потока dpbp для разных ставок дисконтирования:

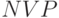Для ставок дисконтирования r=15\% (j=2) и r=30\% (j=3), r=45\% (j=4) NVP меняет знак на 4 квартал, для 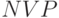r=60\% NVP отрицательная.

dpbp_2:=4+\frac{(-NVP)_{4,2}}{DCH_{5,2}}, dpbp_3:=4+\frac{(-NVP)_{4,3}}{DCH_{5,3}}, dpbp_4:=4+\frac{(-NVP)_{4,4}}{DCH_{5,4}}

r=15\% dpbp_2=4.1 кварталов dpbp_2\cdot 3=12.3 месяцев

r=30\% dpbp_3=4.4 кварталов dpbp_3\cdot 3=13.3 месяцев

r=45\% dpbp_4=4.8 кварталов dpbp_4\cdot 3=14.5 месяцев

Краткие итоги

Приведены основные финансовые параметры. Изложены схемы простых и сложных процентов. Приведены математические формулы, по которым производится расчет финансовых показателей. В Mathcad проведены расчеты основных финансовых параметров для разных финансовых потоков. Показано построение модели финансовой задачи. Все вычисления представлены в матричном виде. Расчеты проведены по формулам и по финансовым функциям. Построены графики результатов.

Ключевые термины

Финансовая математика — раздел прикладной математики, имеющий дело с финансовыми расчётами. В финансовой математике любой финансовый инструмент рассматривается с точки зрения генерируемого этим инструментом некоторого денежного потока.

Денежный поток - (Cash Flow) - поток наличных денег, важнейшее понятие современного финансового анализа.

Финансовые функции – специальные функции для расчета параметров денежных потоков на основе алгоритма сложных процентов, применяются при планировании и анализе финансово-хозяйственной деятельности предприятия, а также при решении задач, связанных с инвестированием средств.

Будущая стоимость – сумма долга (инвестиции) с начисленными процентами в конце срока.

Текущая стоимость - исходная сумма долга (инвестиции) или оценка современной величины денежной суммы, поступление которой ожидается в будущем, в пересчете на более ранний момент времени.

Процентная ставка - относительный показатель эффективности вложений (норма доходности), характеризует темп прироста стоимости за период.

Сложные проценты - схема начисления процентов к исходной сумме долга (инвестиции) с капитализацией процентов, то есть на следующий период проценты начисляются к наращенной сумме.

Элементарный денежный поток - денежный поток без дополнительных или периодических выплат.

Эффективная процентная ставка - ставка, обеспечивающая то же значение наращенной суммы при одноразовом в течение года начислении процентов, как и m - разовое с периодической ставкой r/m

Финансовая рента - поток положительных платежей, через одинаковые интервалы времени, если платежи одинаковые – постоянная рента.

Математическое дисконтирование - переоценка будущего платежа на более ранний момент времени.

Ставка дисконтирования - процентная ставка r, с учетом которой оценивается современная стоимость.

Чистая дисконтированная стоимость - показывает, насколько современная стоимость текущих платежей (доходов и вложений) превышает инвестиционные затраты I в начальный момент времени,

Нерегулярный денежный поток – поток неравных платежей.

Инвестиционный проект – комплекс действий (работ, услуг, управленческих операций и решений), направленных для осуществления действий, связанных с размещением капитала.

Внутренняя норма доходности ставка r, при которой все дисконтированные положительные выплаты (доходы), начальная инвестиция I и дисконтированные отрицательные выплаты (затраты) уравниваются.

Срок окупаемости минимальный временной период, за который инвестиция и доходы перекрывают все расходы

Дальше >>
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Вопросы и ответы

вопросов: 0