НОУ ИНТУИТ | Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования. Лекция 2: Финансово-экономические модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Уральский государственный экономический университет

Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 467 / 49 | Длительность: 11:44:00

Темы: Математика, Экономика, Образование

|

Вам нравится? Нравится 25 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Лекция знакомит с методами финансово-экономического моделирования средствами программы Mathcad. Описаны денежные потоки разного вида: элементарный (простейший) поток, состоящий из одной выплаты и последующего поступления, постоянная финансовая рента, регулярный поток. Приведены математические выражения для основных показателей финансовых потоков, которые лежат в основе финансовых функций. На примерах показано проведение финансовых расчетов двумя способами: по математическим формулам и с использованием встроенных финансовых функций. Все задачи решаются в матричном виде. Результаты представляются в виде графиков.

Цель лекции. Показать построение финансовой модели: как выделить данные и как построить решение. Научить работать с данными и функциями в матричном виде, использовать финансовые функции для индексных переменных. Продемонстрировать представление результатов в виде графиков.

2.1. Постановка финансовой задачи

Финансовая математика изучает соотношения между размерами платежей, сроками выплат и процентными ставками, возникающими в коммерческих сделках и финансово-банковских операциях [8,9,10]. Начиная с версии системы Mathcad 2001 PRO/Premium, в программу введен пакет финансовых функций. Любая из финансово-экономических функций предназначена для вычисления значения одного из финансовых параметров -экономических расчетов по заданным значениям других параметров Расчеты будем производить, используя математические формулы и встроенные финансовые функции. Проведем финансовые расчеты с использованием программы Mathcad [11,12].

Простейшей финансовой операцией является предоставление в долг в некоторый начальный момент суммы 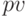с условием, что будет возвращена сумма 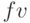. Эффективность такой операции определяется процентной ставкой r=(fv– pv)/pv . Доходность денег зависит от длительности их использования. Время в финансовых вычислениях измеряется в периодах.

Основные финансовые параметры:

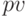(present value) – текущая стоимость– исходная сумма долга или оценка современной величины денежной суммы, поступление которой ожидается в будущем, в пересчете на более ранний момент времени.
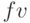(future value) – будущая стоимость – сумма долга с начисленными процентами в конце срока.
– процентная ставка - относительный показатель эффективности вложений (норма доходности), характеризует темп прироста стоимости за период.
(number of periods) –число расчетных периодов – равных по длине подынтервалов времени, в конце которых регулярно начисляются проценты.
– срок, по истечении которого сумму долга и проценты нужно вернуть, измеряется, как правило, в годах. Если –число раз начисления процентов в году, ,
– периодический платеж ренты.

В финансовой практике используются различные схемы. Схема простых процентов предполагает начисление процентов к базовому капиталу 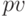за срок nper . Будущая стоимость составляет

$fv=pv\cdot (1+r\cdot nper)$

( 2.1)

Наращенная стоимость является линейной функцией от ставки. Вычисления в схеме простых процентов элементарны. Простые проценты используются при краткосрочных операциях.

Сложные проценты начисляются по ставке на сумму, которая растет. После каждого начисления процентов осуществляется их капитализация, то есть на следующий период проценты начисляются к наращенной сумме. Математические выражения имеют вид степенных функций, вычисления по схеме сложных процентов более сложные. Разработана целая серия финансовых функций. В них заложен алгоритм схемы сложных процентов. Любая из финансово-экономических функций предназначена для вычисления значения одного из финансовых параметров экономических расчетов по заданным значениям других параметров. Некоторые финансовые функции, используемые в задачах, приведены в приложении. Рассмотрим расчеты финансовых параметров для разных видов денежных потоков по схеме сложных процентов.

2.2. Элементарный денежный поток

Элементарный денежный поток - денежный поток без дополнительных или периодических выплат. Рассматриваем схему сложных процентов[[8,9]. Пусть проценты начисляются раз в год. Поскольку начисление процентов идет на наращенную сумму, будущая стоимость за n лет составит.

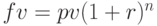( 2.2)

Сумма растет по закону геометрической прогрессии с постоянным знаменателем (1+r) . Пусть сумма 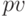вложена на лет с начислением процентов раз в год. Чем больше количество начислений , тем больше наращенная стоимость 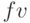. Проделав несложные преобразования, получаем выражения для других финансовых величин:

$fv=pv(1+r/m)^{nm}$

( 2.3)

$pv=fv/(1+r/m)^{mn}$

( 2.4)

$r=m[(fv/pv)^{1/mn}-1]$

( 2.5)

$nper =\ln(fv_n/pv)/\ln(1+r/m)$

( 2.6)

Вычислению каждой финансовой величины соответствует соответствующая финансовая функция.

Эффективная процентная ставка

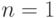Годовая ставка, обеспечивающая то же значение наращенной суммы при одноразовом в течение года начислении процентов, что и - разовое с периодической ставкой r/m называется эффективной ставкой. Вкладывая одну денежную единицу pv=1 на 1 год ( n=1 ) при частоте начисления раз в год получаем

$r=(fv-1)/1=1\cdot(1+r/m)^{1\cdot m}-1=(1+r/m)^m-1=r_{eff}$

( 2.7)

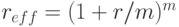$r_{eff}=(1+r/m)^m$

( 2.8)

$r_{eff}$ - эффективный годовой процент, получаемый при вложении за один год.

С введенной эффективной ставкой формулы ( 2.3-2.6) имеют вид

$fv=pv(1+r_{eff})^n$

( 2.9)

$pv=fv_n/(1+r_{eff})^n$

( 2.10)

$r=m[(fv/pv)^{\frac{1}{mn}}-1]$

( 2.11)

$n=\log(fv_n/pv)/\log(1+r_{eff})$

( 2.12)

Непрерывное наращение

Проценты могут начисляться даже чаще, чем один раз в день. При бесконечно частом $m\to \infty$ ) дроблении года на малые процентные периоды, то есть при непрерывном наращении сложных процентов получается показательный закон роста

$fv=pv \lim_{m \to \infty}(1+r/m)^m=pv\cdot e^r$

( 2.13)

Процентную ставку , являющуюся показателем степени в формуле множителя непрерывного наращения, называют интенсивностью или силой роста. Она связана с годовой эффективной ставкой процента $r_{eff}$ соотношением

$e^r=r_{eff}$

( 2.14)

Примеры решения задач

Проведем ряд финансовых расчетов двумя способами: по математическим формулам, приведенным выше, и с использованием встроенных финансовых функций. Проанализируем, как работают финансовые функции в MathCAD. Если входные величины даны в виде ряда значений, представляем их векторами. Рассчитанные финансовые величины также имеем также в виде векторов. Альтернативно используем встроенные финансовые функции. Результаты демонстрируем в графическом виде.

Дальше >>

Авторизоваться

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Финансово-экономические модели

2.1. Постановка финансовой задачи

2.2. Элементарный денежный поток

Эффективная процентная ставка

Непрерывное наращение

Примеры решения задач

Вопросы и ответы