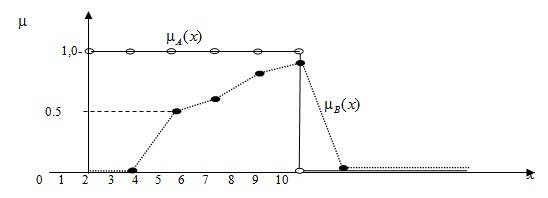
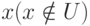Нечеткие множества
Цель лекции. Познакомить с нечеткими множествами. Научить ставить задачу для построения нечетко-множественной модели. Показать, как строить нечеткие множества и производить действия над ними в Mathcad. Представить методы решения нечетко-множественной модели в процессе решения задач.
6.1 Нечетко-множественное моделирование
При моделировании широкого класса реальных объектов возникают необходимость принимать решения в условиях неполной нечеткой информации. Современным перспективным направлением моделирования различного вида неопределенностей является теория нечетких множеств. В рамках теории нечетких множеств разработаны методы формализации и моделирования рассуждений человека, таких понятий как "более или менее высокий уровень инфляции", "устойчивое положение на рынке", "более ценный" и т.д.
Впервые понятие нечетких множеств предложил американский ученый Л.А.Заде (1965 г ). Его идеи послужили развитию нечеткой логики . В отличие от стандартной логики с двумя бинарными состояниями (1/0, Да/Нет, Истина/Ложь), нечеткая логика позволяет определять промежуточные значения между стандартными оценками. Примерами таких оценок являются: "скорее да, чем нет", "наверное да", "немного вправо", "резко влево" в отличие от стандартных: "вправо" или "влево", "да". В теории нечетких множеств введены нечеткие числа как нечеткие подмножества специализированного вида, соответствующих высказываниям типа "значение переменной примерно равно а". В качестве примера рассмотрим треугольное нечеткое число, где выделяются три точки: минимально возможное, наиболее ожидаемое и максимально возможное значение фактора. Треугольные числа – это самый часто используемый на практике тип нечетких чисел, причем, чаще всего их используют в качестве прогнозных значений параметра. Например, ожидаемое значение инфляции на следующий год. Пусть наиболее вероятное значение – 10%, минимально возможное – 5%, а максимально возможное – 20%, тогда все эти значения могут быть сведены к виду нечеткого подмножества или нечеткого числа A: А: (5, 10, 20)
С введением нечетких чисел оказалось возможным прогнозировать будущие значения параметров, которые меняются в установленном расчетном диапазоне. Вводится набор операций над нечеткими числами, которые сводятся к алгебраическим операциям с обычными числами при задании определенного интервала достоверности (уровня принадлежности). Применение нечетких чисел позволяет задавать расчетный коридор значений прогнозируемых параметров. Тогда ожидаемый эффект оценивается экспертом также как нечеткое число со своим расчетным разбросом (степенью нечеткости).
Нечеткая логика, как модель человеческих мыслительных процессов, встроена в системы искусственного интеллекта и в автоматизированные средства поддержки принятия решений (в частности, в системы управления технологическими процессами).
6.2 Основные понятия теории нечетких множеств
Множество — неопределяемое понятие математики. Георг Кантор (1845 – 1918) – немецкий математик, чьи работы лежат в основе современной теории множеств, дает такое понятие: "…множество — это многое, мыслимое как единое".
Множество, включающее в себя все объекты, рассматриваемые в задаче, называют универсальным множеством. Универсальное множество принято обозначать буквой  . Универсальное множество является максимальным множеством в том смысле, что все объекты являются его элементами, т.е. утверждение
. Универсальное множество является максимальным множеством в том смысле, что все объекты являются его элементами, т.е. утверждение 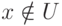 в рамках задачи всегда истинно. Минимальным множеством является пустое множество –
в рамках задачи всегда истинно. Минимальным множеством является пустое множество –  , которое не содержит ни одного элемента. Все остальные множества в рассматриваемой задаче являются подмножествами множества
, которое не содержит ни одного элемента. Все остальные множества в рассматриваемой задаче являются подмножествами множества  . Напомним, что множество
. Напомним, что множество  называют подмножеством множества
называют подмножеством множества  , если все элементы
, если все элементы  являются также элементами
являются также элементами  . Задание множества
. Задание множества  — это правило, позволяющее относительно любого элемента
— это правило, позволяющее относительно любого элемента  универсального множества
универсального множества  однозначно установить, принадлежит
однозначно установить, принадлежит  множеству
множеству  или не принадлежит. Другими словами, это правило, позволяющее определить, какое из двух высказываний,
или не принадлежит. Другими словами, это правило, позволяющее определить, какое из двух высказываний, 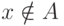 или
или 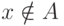 , является истинным, а какое ложным. Одним из способов задания множеств является задание с помощью характеристической функции.
, является истинным, а какое ложным. Одним из способов задания множеств является задание с помощью характеристической функции.
Характеристической функцией множества  называют функцию
называют функцию  , заданную на универсальном множестве
, заданную на универсальном множестве  и принимающую значение единица на тех элементах множества
и принимающую значение единица на тех элементах множества  , которые принадлежат
, которые принадлежат  , и значение нуль на тех элементах, которые не принадлежат
, и значение нуль на тех элементах, которые не принадлежат  :
:
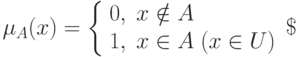 |
( 6.1) |
В качестве примера рассмотрим универсальное множество 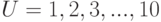 и два его подмножества:
и два его подмножества:  — множество чисел, меньших 7, и
— множество чисел, меньших 7, и  — множество чисел, немного меньших 7. Характеристическая функция множества
— множество чисел, немного меньших 7. Характеристическая функция множества  имеет вид
имеет вид
 |
( 6.2) |
Множество  в данном примере является обычным множеством.
в данном примере является обычным множеством.
Записать характеристическую функцию множества  , используя лишь 0 и 1, невозможно. Например, включать ли в
, используя лишь 0 и 1, невозможно. Например, включать ли в  числа 1 и 2? "намного" или "ненамного" число 3 меньше 7? Ответы на эти и подобные им вопросы могут быть получены в зависимости от условий задачи, в которой используются множества
числа 1 и 2? "намного" или "ненамного" число 3 меньше 7? Ответы на эти и подобные им вопросы могут быть получены в зависимости от условий задачи, в которой используются множества  и
и  , а также от субъективного взгляда того, кто решает эту задачу. Множество
, а также от субъективного взгляда того, кто решает эту задачу. Множество  называется нечетким множеством. При составлении характеристической функции нечеткого множества
называется нечетким множеством. При составлении характеристической функции нечеткого множества  решающий задачу (эксперт) может высказать свое мнение относительно того, в какой степени каждое из чисел множества
решающий задачу (эксперт) может высказать свое мнение относительно того, в какой степени каждое из чисел множества  принадлежит множеству
принадлежит множеству  . В качестве степени принадлежности можно выбрать любое число с отрезка
. В качестве степени принадлежности можно выбрать любое число с отрезка ![[0, 1]](/sites/default/files/tex_cache/264884439b70ab09a86bc848421c6de6.png) . При этом
. При этом 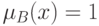 означает полную уверенность эксперта в том, что
означает полную уверенность эксперта в том, что 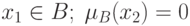 — столь же полную уверенность, что
— столь же полную уверенность, что  говорит о том, что эксперт затрудняется в ответе на вопрос, принадлежит ли
говорит о том, что эксперт затрудняется в ответе на вопрос, принадлежит ли  множеству
множеству  или не принадлежит. Если
или не принадлежит. Если 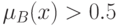 , то эксперт склонен отнести
, то эксперт склонен отнести  к множеству
к множеству  , если же
, если же 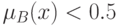 , то не склонен.
, то не склонен.
Функцией принадлежности нечеткого множества  называют функцию
называют функцию  , которая
, которая
- устанавливает значения степени принадлежности нечеткому множеству
 каждого из элементов универсального множества
каждого из элементов универсального множества  и принимает значения на отрезке
и принимает значения на отрезке ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) .
. - позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству
 .
.
Такую функцию называют функцией принадлежности нечеткому множеству  . - Максимальное значение функции принадлежности
. - Максимальное значение функции принадлежности  , присутствующее в множестве - верхняя грань - называется супремум. Функция принадлежности отражает субъективный взгляд специалиста на задачу, вносит индивидуальность в ее решение.
, присутствующее в множестве - верхняя грань - называется супремум. Функция принадлежности отражает субъективный взгляд специалиста на задачу, вносит индивидуальность в ее решение.
Характеристическую функцию  обычного множества
обычного множества  можно рассматривать как функцию принадлежности этому множеству, но в отличие от нечеткого множества,
можно рассматривать как функцию принадлежности этому множеству, но в отличие от нечеткого множества,  принимает лишь два значения: 0 или 1.
принимает лишь два значения: 0 или 1.
Нечетким множеством  называют пару
называют пару 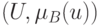 , где
, где  — универсальное множество,
— универсальное множество,  — функция принадлежности нечеткого множества
— функция принадлежности нечеткого множества  .
.
Несущим множеством или носителем нечеткого множества  называют подмножество множества
называют подмножество множества  , состоящее из элементов, на которых
, состоящее из элементов, на которых 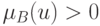 .
.
Точкой перехода нечеткого множества  называют элемент множества
называют элемент множества  , на котором
, на котором 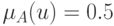 .
.
В рассматриваемом примере, где 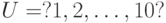 ,
,  — множество чисел, меньших 7,
— множество чисел, меньших 7,  — множество чисел, немного меньших 7, субъективно выбираем значения для множества
— множество чисел, немного меньших 7, субъективно выбираем значения для множества  , которые будут составлять функцию принадлежности
, которые будут составлять функцию принадлежности  . В таблице 6.1 представлены функции принадлежности
. В таблице 6.1 представлены функции принадлежности  и
и  для
для  и
и  .
.
Часто используется более компактная запись конечных или счетных нечетких множеств. Так, вместо приведенного выше табличного представления подмножеств  и
и  , эти подмножества можно записать следующим образом:
, эти подмножества можно записать следующим образом:
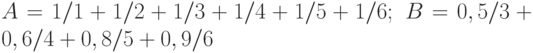
В приведенных равенствах указаны значения функции принадлежности для соответствующих элементов множества  , знак "+" означает объединение одноэлементных подмножеств
, знак "+" означает объединение одноэлементных подмножеств  , для которых значения функции принадлежности больше нуля. Такое объединение называют несущим множеством или носителем соответствующего нечеткого множества. Так, несущее множество для
, для которых значения функции принадлежности больше нуля. Такое объединение называют несущим множеством или носителем соответствующего нечеткого множества. Так, несущее множество для  состоит из чисел:
состоит из чисел: 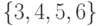 .
.
Нечеткое множество  записывают в виде (1.2), если
записывают в виде (1.2), если  , и в виде (1.3), если
, и в виде (1.3), если  непрерывно.
непрерывно.
Общая форма записи нечеткого подмножества для случаев, когда U дискретно имеет вид:
 |
( 6.3) |
В общем случае нечеткое множество B с непрерывным носителем U обозначается
 |
( 6.4) |
В выражениях (6.3) и (6.4), как правило, указываются лишь элементы несущего множества. Использование символа интеграла не означает интегрирования, но предполагает, объединение по всем элементам несущего множества  . Знак интеграла показывает, что несущее множество является частью числовой оси.
. Знак интеграла показывает, что несущее множество является частью числовой оси.
Элемент множества  , на котором значение функции принадлежности равно 0.5, называют точкой перехода. Точкой перехода для множества
, на котором значение функции принадлежности равно 0.5, называют точкой перехода. Точкой перехода для множества  в рассмотренном выше примере является
в рассмотренном выше примере является 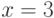 . Точка перехода – это точка, о которой мнение эксперта можно выразить словами "неизвестно", "не определено" и т.п. Если функция принадлежности нечеткого множества достигает 1, то множество называют нормальным, если не достигает — субнормальным. Поскольку в разобранном примере ни одно из значений
. Точка перехода – это точка, о которой мнение эксперта можно выразить словами "неизвестно", "не определено" и т.п. Если функция принадлежности нечеткого множества достигает 1, то множество называют нормальным, если не достигает — субнормальным. Поскольку в разобранном примере ни одно из значений  не достигло своего возможного максимального значения – 1, то
не достигло своего возможного максимального значения – 1, то  – нечеткое субнормальное множество. Субнормальное множество можно нормировать, разделив все значения функции принадлежности на ее наибольшее значение. Множество
– нечеткое субнормальное множество. Субнормальное множество можно нормировать, разделив все значения функции принадлежности на ее наибольшее значение. Множество  после нормирования примет следующий вид:
после нормирования примет следующий вид: 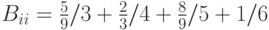 .
.
Удобно представление нечетких множеств в виде графиков функций принадлежности  (рис.6.1).
(рис.6.1).