Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Уральский государственный экономический университет
Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 467 / 49 | Длительность: 11:44:00
Темы: Математика, Экономика, Образование
Лекция 6:

Нечеткие множества

A
|
версия для печати
< Лекция 5 || Лекция 6: 123456789

Анализ решения

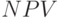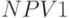Выберем достоверные значения полученного нечеткого множества NPV. Для этого построим для него множество, ближайшее к нечеткому (определение (6.7)). Перестроим матрицы NPV0 и NPV1 в множества ближайшие к нечетким в соответствии с определением (6.7). Это будут две матрицы NPVd и NPVd1 для правого и левого края сечения. Второй столбец – значения характеристической функции \mu. Используем средства программирования Mathcad и условную функцию if .

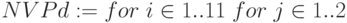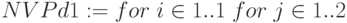
NVPd:=for\; i\in 1..11 \; for \; j\in 1..2, NVPd1:=for\; i\in 1..1 \; for \; j\in 1..2

\begin{array}{|lc} [NPVd_{i,j}\leftarrow (NPV0_{i,j})] \\ continue \; if\; j=1 \\ NPVd_{i,j}\leftarrow 0 \; if \; (NPV0_{i,2}\le 0.5) \\ NPVd_{i,j}\leftarrow 1 \; if \; NPV0_{i,2}> 0.5 \\ NPVd \end{array}

\begin{array}{|lc} [NPVd1_{i,j}\leftarrow (NPV1_{i,j})] \\ continue \; if\; j=1 \\ NPVd1_{i,j}\leftarrow 0 \; if \; (NPV1_{i,2}\le 0.5) \\ NPVd1_{i,j}\leftarrow 1 \; if \; NPV1_{i,2}> 0.5 \\ NPVd1 \end{array}

NVPd=\begin{array}{|c|c|c|} \hline & 1 & 2\\ \hline 1 & -0.703 & 0 \\ \hline 2 & -0.61 & 0 \\ \hline 3 & -0.518 & 0 \\ \hline 4 & -0.427 & 0 \\ \hline 5 & -0.338 & 0 \\ \hline 6 & -0.25 & 0 \\ \hline 7 & -0.164 & 1 \\ \hline 8 & -0.078 & 1\\ \hline 9 & 5.731\cdot 10^{-3} & ... \\ \hline \end{array}

NVPd1=\begin{array}{|c|c|c|} \hline & 1 & 2\\ \hline 1 & 0.976 & 0 \\ \hline 2 & 0.899 & 0 \\ \hline 3 & 0.822 & 0 \\ \hline 4 & 0.743 & 0 \\ \hline 5 & 0.664 & 0 \\ \hline 6 & 0.584 & 0 \\ \hline 7 &0.503 & 1 \\ \hline 8 & 0.422 & 1\\ \hline 9 & 0.339 & 1 \\ \hline 10 & 0.255 & ...\\ \hline \end{array}

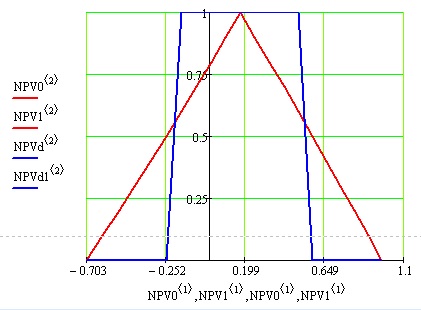
График функции принадлежности нечеткого множества NPV0 и NPV1 и множества ближайшего к нечеткому NPVd и NPVd1

Рис. 6.20. График функции принадлежности нечеткого множества NPV0 и NPV1 и множества ближайшего к нечеткому NPVd и NPVd1

На графике множество, ближайшее к нечеткому – прямоугольная функция. Достоверные значения NPV^{(1)} соответствуют ординате, равной 1.

Перепишем множества, ближайшие к нечетким NPVd и NPVd1 вместе с характеристической функцией и значениями ? в одну матрицу NPVn с помощью функций, изменяющих структуру матриц: augment () ,\; stack() и функции сортировки csort( ).

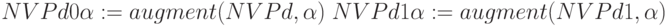
NVPd0\alpha:=augment(NVPd,\alpha)\; NVPd1\alpha:=augment(NVPd1,\alpha)

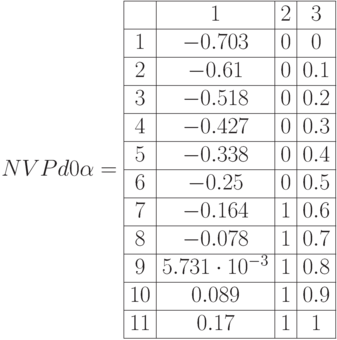
NVPd0\alpha=\begin{array}{|c|c|c|с|} \hline & 1 & 2& 3\\ \hline 1 & -0.703 & 0 & 0 \\ \hline 2 & -0.61 & 0 & 0.1 \\ \hline 3 & -0.518 & 0 & 0.2\\ \hline 4 & -0.427 & 0 & 0.3\\ \hline 5 & -0.338 & 0 & 0.4 \\ \hline 6 & -0.25 & 0 & 0.5 \\ \hline 7 & -0.164 & 1 & 0.6 \\ \hline 8 & -0.078 & 1 & 0.7\\ \hline 9 & 5.731\cdot 10^{-3} & 1 & 0.8 \\ \hline 10 & 0.089 & 1 & 0.9 \\ \hline 11 & 0.17 & 1 & 1 \\ \hline \end{array}

NVPd1\alpha=\begin{array}{|c|c|c|c|} \hline & 1 & 2 & 3\\ \hline 1 & 0.976 & 0 & 0 \\ \hline 2 & 0.899 & 0 & 0.1 \\ \hline 3 & 0.822 & 0 & 0.2\\ \hline 4 & 0.743 & 0 & 0.3 \\ \hline 5 & 0.664 & 0 & 0.4 \\ \hline 6 & 0.584 & 0 & 0.5\\ \hline 7 &0.503 & 1 & 0.6 \\ \hline 8 & 0.422 & 1 & 0.7\\ \hline 9 & 0.339 & 1 & 0.8\\ \hline 10 & 0.255 & 1 & 0.9\\ \hline 11 & 0.17 & 1 & 1 \\ \hline \end{array}

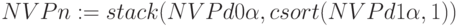
NVPn:=stack(NVPd0\alpha,csort(NVPd1\alpha,1))

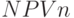Матрица NPVn всех значений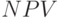 NPV

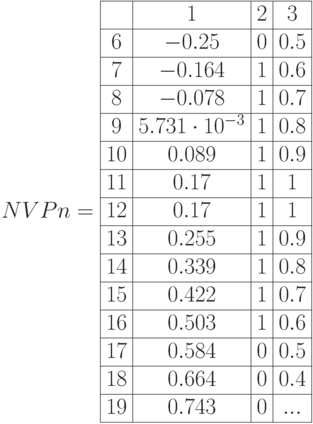
NVPn=\begin{array}{|c|c|c|c|} \hline & 1 & 2 & 3\\ \hline 6 & -0.25 & 0 & 0.5 \\ \hline 7 & -0.164 & 1 & 0.6 \\ \hline 8 & -0.078 & 1 & 0.7\\ \hline 9 & 5.731\cdot 10^{-3} & 1 & 0.8 \\ \hline 10 & 0.089 & 1 & 0.9 \\ \hline 11 & 0.17 & 1 & 1\\ \hline 12 & 0.17 & 1 & 1 \\ \hline 13 & 0.255 & 1 & 0.9\\ \hline 14 & 0.339 & 1 & 0.8\\ \hline 15 & 0.422 & 1 & 0.7\\ \hline 16 & 0.503 & 1 & 0.6 \\ \hline 17 & 0.584 & 0 & 0.5 \\ \hline 18 & 0.664 & 0 & 0.4 \\ \hline 19 & 0.743 & 0 & ... \\ \hline \end{array}

Достоверные значения 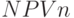NPVn соответствуют значениям характеристической функции 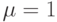\mu=1. Построим матрицу достоверных значений 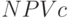NPVc с значениями уровней \alpha. Используем блок программирования.

m:=1

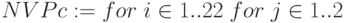
NVPc:=for\; i\in 1..22 \; for \; j\in 1..2

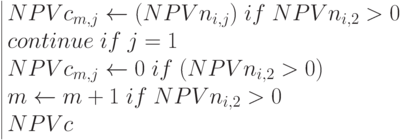
\begin{array}{|lc} NPVc_{m,j}\leftarrow (NPVn_{i,j})\; if \; NPVn_{i,2}>0 \\ continue \; if\; j=1 \\ NPVc_{m,j}\leftarrow 0 \; if \; (NPVn_{i,2}> 0) \\ m\leftarrow m+1 \; if \; NPVn_{i,2}> 0 \\ NPVc \end{array}

Достоверные значения дисконтированной стоимости 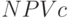NPVc и соответствующие значения \alpha – уровня

NVPc=\begin{array}{|c|c|c|} \hline & 1 & 2 \\ \hline 1 & -0.164 & 0.6 \\ \hline 2 & -0.078 & 0.7 \\ \hline 3 & 5.731\cdot 10^{-3} & 0.8\\ \hline 4 & 0.089 & 0.9 \\ \hline 5 & 0.17 & 1 \\ \hline 6 & 0.17 & 1\\ \hline 7 & 0.255 & 0.9 \\ \hline 8 & 0.339 & 0.8\\ \hline 9 & 0.422 & 0.7\\ \hline 10 & 0.503 & 0.6\\ \hline \end{array}

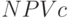Массив NPVc – решение задачи. Проект является прибыльным, если 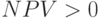NPV >0 для выбранной ставки дисконтирования .. Тогда исследуемый инвестиционный проект можно принять, если 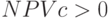NPVc>0. Эти значения реализуются для 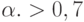\alpha.>0,7. Соответствующие значения начальной инвестиции 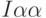I\alpha\alpha могут быть в пределах от 2,97 до 3,03 млн. руб., тогда можно получить прибыль в год от 1,79 до 2,21 млн. руб., при ставке дисконтирования от 16% до 18%.

Дальше >>
< Лекция 5 || Лекция 6: 123456789

Вопросы и ответы

вопросов: 0