Оптимизационные модели
Цель лекции. Научить строить математическую модель оптимизационных задач средствами Mathcad. Выделять управляемые переменные, целевую функции. ограничения, затем строить систему уравнений. Применять блок given - maximize (minimize) для решения матричных уравнений. Анализировать полученное решение. Строить графики результата.
4.1. Постановка оптимизационной задачи
Принятию любого экономического или финансового решения предшествует перебор и оценка вариантов. Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными [18, 19].
Типы оптимизационных задач в экономике:
- Задачи оптимального планирования деятельности предприятий.
- Задачи оптимального прикрепления потребителей к поставщикам - транспортная.
- Задачи оптимального распределения трудовых ресурсов.
- Задача оптимального составления смесей
- Бинарные задачи распределения.
- Задачи формирования оптимального портфеля ценных бумаг (инвестиционных проектов).
Оптимизационные задачи решаются с помощью оптимизационных моделей. Оптимизационные модели возникают при практической реализации принципа оптимальности в управлении. В каждом случае выделяется объект оптимизации, определяется цель оптимизации, ставится задача нахождения экстремума функции, описывающей оптимизируемую цель при заданных условиях. Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. В качестве инструмента используется математическое программирование (планирование): линейное, нелинейное, динамическое, и т.п. В зависимости от типа переменных и функциональных связей различают задачи линейного и нелинейного программирования. Многие экономические задачи формулируются в терминах линейного программирования, поскольку функции прибыли, стоимости затрат - линейные функции переменных, связанных с объемами выпуска, продаж и других факторов.
В общем виде задача линейного программирования ЗЛП ставится следующим образом: найти вектор 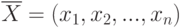 , максимизирующий (минимизирующий) линейную форму
, максимизирующий (минимизирующий) линейную форму 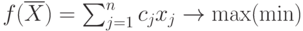 , удовлетворяющий условиям:
, удовлетворяющий условиям:
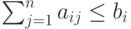 |
( 4.1) |
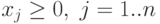 |
( 4.2) |
где  — заданная функции,
— заданная функции, 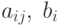 — некоторые действительные числа.
— некоторые действительные числа.
Линейная функция 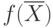 - целевая функция задачи, условия ( 4.1) (4.2) - ограничения задачи, вектор
- целевая функция задачи, условия ( 4.1) (4.2) - ограничения задачи, вектор 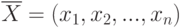 , компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, называется планом или допустимым решением ЗЛП. Допустимое решение, максимизирующее (минимизирующее) целевую функцию
, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, называется планом или допустимым решением ЗЛП. Допустимое решение, максимизирующее (минимизирующее) целевую функцию 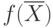 , называется оптимальным планом задачи:
, называется оптимальным планом задачи: 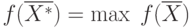 (или
(или  ) где
) где 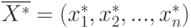 - оптимальное решение ЗЛП.
- оптимальное решение ЗЛП.
В оптимизационной задаче экономический показатель, для которого определяется максимальное или минимальное значение - целевая функция. Управляемые переменные - аргументы целевой функции - переменные задачи, которые подвергаются изменению в процессе поиска решения. Область допустимых решений – это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.
Приведем примеры экономико-математического моделирования оптимизационных задач средствами Mathcad.
4.2.Оптимальное планирование выпуска продукции
Рассмотрим классическую задачу формирования производственной программы [20,21,22]. Пусть осуществляется выпуск  видов продукции. Для этого используется n основных видов ресурсов
видов продукции. Для этого используется n основных видов ресурсов  , (механизмов, оборудования, времени, специалистов), объем которых на предприятии задан. Известно количество каждого ресурса, идущего на выпуск единицы продукции каждого вида. Отдельная продукция реализуется по цене c, норма переменных затрат для нее составляет
, (механизмов, оборудования, времени, специалистов), объем которых на предприятии задан. Известно количество каждого ресурса, идущего на выпуск единицы продукции каждого вида. Отдельная продукция реализуется по цене c, норма переменных затрат для нее составляет  . Необходимо, чтобы производственная программа была оптимальна и давала наибольшую валовую прибыль,
. Необходимо, чтобы производственная программа была оптимальна и давала наибольшую валовую прибыль,
Постановка задачи. Цель моделирования – получить максимальную прибыль, которая определяется количеством произведенной продукции в имеющихся условиях с учетом всех ограничений. Найти вариант из множества возможных.
Модель задачи
Определение переменных. Введем обозначения:
Входные переменные:
 –видов продукции,
–видов продукции,  – текущий номер вида продукции.
– текущий номер вида продукции.
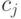 - прибыль от реализации единицы
- прибыль от реализации единицы  -го вида продукции.
-го вида продукции.
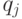 - переменные затраты производства единицы
- переменные затраты производства единицы  -го вида продукции
-го вида продукции
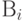 - запасы
- запасы  -го ресурса
-го ресурса  – текущий номер вида ресурса,
– текущий номер вида ресурса,  - количество ресурсов.
- количество ресурсов.
 - норма затрат
- норма затрат  го ресурса для производства
го ресурса для производства  -го вида продукции
-го вида продукции
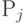 – требуемое количество выпуска продукции каждого вида по плану,
– требуемое количество выпуска продукции каждого вида по плану,
Выходные показатели – суммарная прибыль  ,
,
Управляемые переменные.  - искомый объем продукции
- искомый объем продукции  -го вида.
-го вида.
Целевая функция – показатель, который определяет цель моделирования - результирующий, оптимизируемый параметр – прибыль. Цель решения задачи – нахождение значений управляемых переменных  , доставляющих экстремум целевой функции прибыли
, доставляющих экстремум целевой функции прибыли  .
.
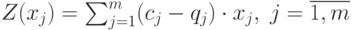 |
( 4.3) |
 |
( 4.4) |
Ограничения. условия, налагаемые на данные задачи, определяющие исследуемую величину, которая оптимизируется. Различают три типа ограничений:
-
Ресурсные ограничения - ограниченность имеющихся ресурсов; обеспечивающих выпуск:
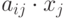 – планируемые затраты ресурса
– планируемые затраты ресурса  для производства продукции
для производства продукции  ,
, – планируемые затраты ресурса
– планируемые затраты ресурса  на производство всех видов продукции,
на производство всех видов продукции, - условие ограниченности ресурсов
- условие ограниченности ресурсов -
плановые ограничения - необходимость выполнения заданных значений
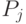 для искомых объемов продукции
для искомых объемов продукции  -го вида:
-го вида: 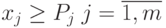 - условие ограниченности по плану
- условие ограниченности по плану -
технологические соотношения между группами управляемых переменных, здесь
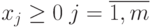
Уравнения. В результате имеем систему уравнений, которую надо решить.
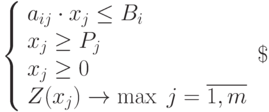 |
( 4.5) |
Решение, если получено, представляется в виде оптимального решения. Это:
количество управляемых переменных, не равных нулю,
числовые значения управляемых переменных,
полученное значение целевой функции
Рассмотрим решение модели на примере следующей задачи.
