Оптимизационные модели
1. Выполнение части плана из имеющихся ресурсов
Решение задачи 4.3 в комплектной постановке. Задача - определить, какую часть плана можно выполнить при имеющихся ресурсах. Для этого случая воспользуемся моделью, приведенной в [21]. Ставится цель определения максимальной доли выпуска требуемого плана при имеющихся ресурсах. Разработана "комплектная" постановка задачи. Вводится новая переменная  – возможный процент достижения плана, определяется ее оптимальное значение при уменьшенном плане, ресурсные и технологические ограничения задачи записываются без изменений.: Целевая функция
– возможный процент достижения плана, определяется ее оптимальное значение при уменьшенном плане, ресурсные и технологические ограничения задачи записываются без изменений.: Целевая функция 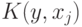 строится как функция двух аргументов: скаляра
строится как функция двух аргументов: скаляра  и вектора переменных продукции
и вектора переменных продукции 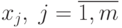 , который неявно зависит от
, который неявно зависит от  . .Решение получается в виде вектора
. .Решение получается в виде вектора 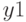 с элементами
с элементами 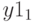 - .найденная доля выполнения плана и
- .найденная доля выполнения плана и 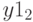 .- найденный вектор переменных продукции.
.- найденный вектор переменных продукции.
Система уравнений в "комплектной" постановке
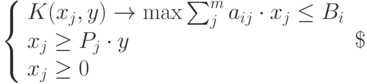 |
( 4.6) |
Ниже приведен листинг решения в MathCad (комплектная постановка).
Входные данные
 - цена реализации
- цена реализации
 - затраты на один компьютер
- затраты на один компьютер
 - прибыль на один компьютер
- прибыль на один компьютер
 - план выпуска
- план выпуска
 – прибыль
– прибыль
Матрица затрат ресурсов: >
Матрица запасов ресурсов: 
Начальные значения:  ,
, 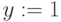
Решение:

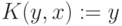 – целевая функция
– целевая функция


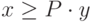
 ,
, 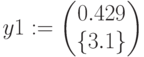
Доля плана: 
Количество выпуска: 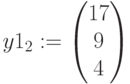
Прибыль: 
Израсходовано ресурсов: 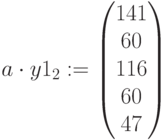
Остаток ресурсов: 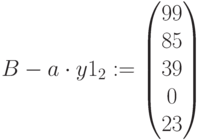
Как видно, план можно выполнен только на 43%, но это оптимальный процент при имеющихся условиях. Полученная прибыль при таком плане еще меньше, чем в задаче 4.2 и ресурсов остается больше.
2. Добавление минимального количества ресурсов для выполнения плана
Решение задачи 4.3 с добавлением ресурсов. Добавление недостающих ресурсов для выполнения полного плана. Воспользуемся t-моделью постановки задачи, представленной в [21], - нахождения минимума дополнительного количества ресурсов, необходимых для выпуска продукции в соответствии с планом. В предлагаемой t-модели вводятся новые переменные  – значения дополнительных ресурсов каждого вида продукции
– значения дополнительных ресурсов каждого вида продукции  . Цель задачи – минимум суммарного количества добавляемых ресурсов. В ресурсные ограничения вводятся дополнительные неизвестные ресурсы, плановые и технологические ограничения вводятся в t-модель без изменений. Целевая функция
. Цель задачи – минимум суммарного количества добавляемых ресурсов. В ресурсные ограничения вводятся дополнительные неизвестные ресурсы, плановые и технологические ограничения вводятся в t-модель без изменений. Целевая функция 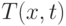 вводится как функция двух аргументов: вектора добавочных ресурсов
вводится как функция двух аргументов: вектора добавочных ресурсов  и вектора переменных продукции
и вектора переменных продукции 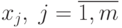 , который неявно зависит от
, который неявно зависит от 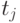
Система уравнений в постановке t -модели
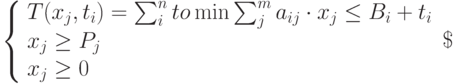 |
( 4.7) |
Листинг решения в Mathcad показан ниже. .Решение получается в виде двумерной переменной 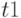 с элементами
с элементами 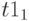 найденный вектор продукции. и
найденный вектор продукции. и 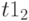 , найденный вектор добавочных ресурсов
, найденный вектор добавочных ресурсов
Далее, имея полученные значения добавочных ресурсов, решаем исходную задачу. На диаграммах показаны старые ресурсы, новые ресурсы. Видны добавочные ресурсы, добавлено ровно столько, чтобы выполнить план. В результате план выполняется и ресурсов не остается
Входные данные
 - цена реализации
- цена реализации
 - затраты на один компьютер
- затраты на один компьютер
 - прибыль на один компьютер
- прибыль на один компьютер
 - план выпуска
- план выпуска
 – прибыль
– прибыль
Матрица затрат ресурсов: >
Матрица запасов ресурсов: 
Начальные значения:  ,
, 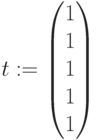
Решение:

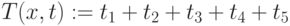 – добавочные ресурсы
– добавочные ресурсы



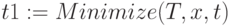
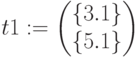
Вектор решений – количество компьютеров: 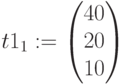
Добавочные ресурсы: 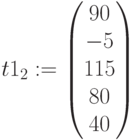
Новые ресурсы: 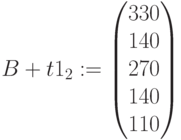
Прибыль: 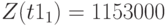
План: 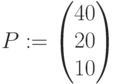
Ресурсы: 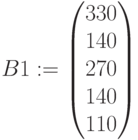
Начальные значения: 

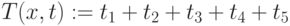 – добавочные ресурсы
– добавочные ресурсы




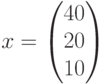 ,
, 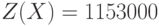
Новые ресурсы: 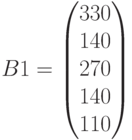
Старые ресурсы: 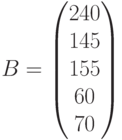
Остаточные ресурсы, новый выпуск: