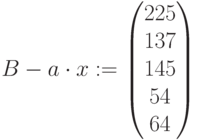Оптимизационные модели
Задача. 4.1.
Фирма по сборке компьютеров предполагает производить выпуск 3 новых моделей при использовании комплектующих 5 типов. Маркетинговые исследования показали возможность сбыта компьютеров по приемлемым продажным ценам. Необходимые данные по запасам комплектующих, и ценам приведены в таблице. Определить оптимальные объемы выпуска компьютеров при имеющихся ресурсах для получения максимальной прибыли.
| Вид комплектующих | Расход комплектующих ед./изд. Модели ПК | Запас комплектующих. (ед.) | ||
| Модель 1 | Модель 2 | Модель 3 | ||
| 1 | 4 | 6 | 5 | 240 |
| 2 | 1 | 3 | 4 | 145 |
| 3 | 5 | 2 | 3 | 155 |
| 4 | 2 | 2 | 2 | 60 |
| 5 | 1 | 2 | 3 | 70 |
| Затраты на 1 изд. | 1800 | 2700 | 2100 | |
| Цена реализации(усл.ед.) | 10000 | 35000 | 20000 | |
Оптимальный выпуск без плана
Решение задачи 4. 1.
Применяем модель, описанную выше. В Mathcad система уравнений с оптимизацией решается численно с помощью блока  и функции
и функции 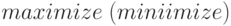 . Задачу решаем в матричном виде: все данные и уравнения представляем в виде матриц. Порядок действий:
. Задачу решаем в матричном виде: все данные и уравнения представляем в виде матриц. Порядок действий:
- ввод данных в виде матриц,
- ввод начальных значений искомых параметров,
- ввод целевой функции,
- в блоке given ввод ограничений,
- ввод функции
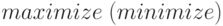 ,
, - получение решения в виде вектора, размер которого равен количеству аргументов целевой функции.
Входные данные
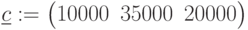 - цена реализации
- цена реализации
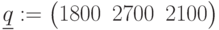 - затраты на один компьютер
- затраты на один компьютер
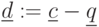 - прибыль на один компьютер
- прибыль на один компьютер
 - прибыль
- прибыль
Затраты ресурсов: 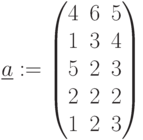
Запасы ресурсов: 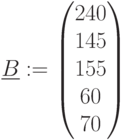
Начальное значение: 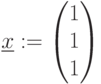
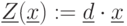

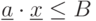

 ,
, 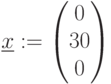
Максимальная прибыль: 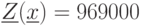
Остаток комплектующих: 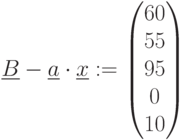
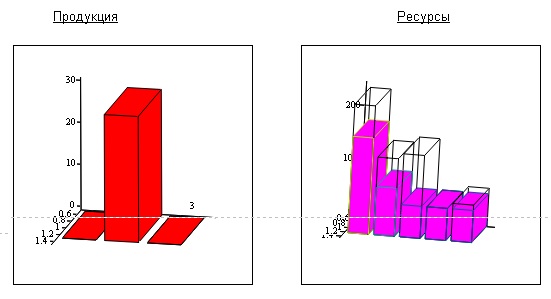
Оптимальный выпуск компьютеров (рис.4.1):
Продукция: 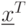
Ресурсы: 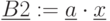
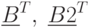
Полученное оптимальное решение (рис. 4.1) следующее. Оптимальная структура выпуска при имеющихся ресурсах без задания плана – 30 компьютеров 2 модели, прибыль при этом составляет 969000 ед. ; 4 вид комплектующих израсходован полностью – это дефицитный ресурс. Остальные ресурсы имеют остаток, они недефицитные.
Проведем экономический анализ: как меняется прибыль при изменении структуры выпуска. Ниже показаны листинги расчета нормированной стоимости. Полученные результаты приведены в таблице. Нормированная стоимость – изменение целевой функции при изменении соответствующего управляемого параметра (количество выпускаемого продукта) на единицу. Нормированная стоимость для модели 1 в 1,7 больше, чем для модели 3.
| Переменная | Результирующее значение | Целевой коэффициент | Нормированная стоимость |
| x1 | 0 | 8200 | 24100 |
| x2 | 30 | 32300 | 0 |
| x3 | 0 | 17900 | 14400 |

Увеличим 1 вид продукции на 1 единицу.
 ,
, 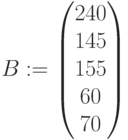 ,
, 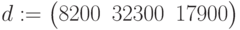 ,
, 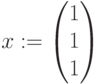
 ,
, 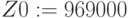 ,
, 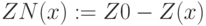 – нормированная стоимость
– нормированная стоимость


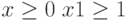

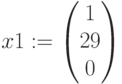
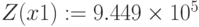 ,
, 
Остаток ресурсов: 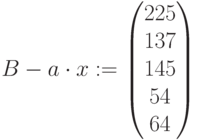
Увеличим 2 вид продукции на 1 единицу


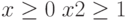

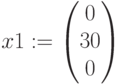
 ,
, 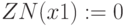
Остаток ресурсов: 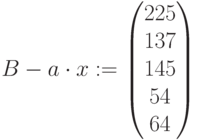
Увеличим 3 вид продукции на 1 единицу


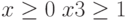

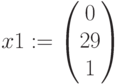
 ,
, 
Остаток ресурсов: