Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Уральский государственный экономический университет
Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 467 / 49 | Длительность: 11:44:00
Темы: Математика, Экономика, Образование
Лекция 6:

Нечеткие множества

A
|
версия для печати
< Лекция 5 || Лекция 6: 123456789

Матрица интервалов достоверности dQ\alpha:

dQ\alpha=\begin{array}{|c|c|c|} \hline & 1 & 2 \\ \hline 1 & -0.05 & 0.08 \\ \hline 2 &-0.046 & 0.074 \\ \hline 3 & -0.042 & 0.068\\ \hline 4 & -0.038 & 0.062 \\ \hline 5 & -0.034 & 0.056 \\ \hline 6 & -0.03 & 0.05\\ \hline 7 & -0.026 & 0.044 \\ \hline 8 & -0.022 & 0.038\\ \hline 9 & -0.018 & 0.032\\ \hline 10 & -0.014 & 0.026\\ \hline 11 & -0.01 & 0.02 \\ \hline \end{array}

P\alpha_{i,1}:=F1P(x)=\alpha_i solve\to 400.0 \cdot \begin{pmatrix} 0 \\ 0.1 \\ 0.2 \\ 0.3 \\ 0.4 \\ 0.5 \\ 0.6 \\ 0.7 \\ 0.8\\ 0.9 \\ 1.0 \end{pmatrix}_i+1400.0

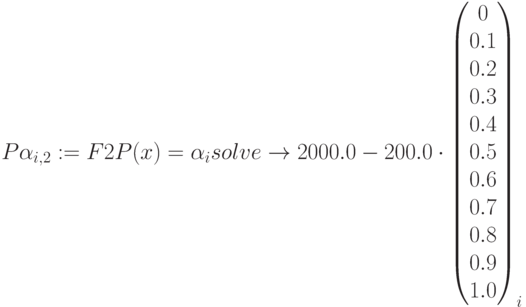
P\alpha_{i,2}:=F2P(x)=\alpha_i solve\to 2000.0-200.0 \cdot \begin{pmatrix} 0 \\ 0.1 \\ 0.2 \\ 0.3 \\ 0.4 \\ 0.5 \\ 0.6 \\ 0.7 \\ 0.8\\ 0.9 \\ 1.0 \end{pmatrix}_i

Матрица интервалов достоверности P\alpha:

P\alpha=\begin{array}{|c|c|c|} \hline & 1 & 2 \\ \hline 1 & 1.4\cdot10^3 & 2\cdot10^3 \\ \hline 2 & 1.4\cdot10^3 & 2\cdot10^3 \\ \hline 3 & 1.5\cdot10^3 & 2\cdot10^3\\ \hline 4 & 1.5\cdot10^3 & 1.9\cdot10^3\\ \hline 5 & 1.6\cdot10^3 & 1.9\cdot10^3 \\ \hline 6 & 1.6\cdot10^3 & 1.9\cdot10^3\\ \hline 7 & 1.6\cdot10^3 & 1.9\cdot10^3 \\ \hline 8 & 1.7\cdot10^3 & 1.9\cdot10^3\\ \hline 9 & 1.7\cdot10^3 & 1.8\cdot10^3\\ \hline 10 & 1.8\cdot10^3 & 1.8\cdot10^3\\ \hline 11 & 1.8\cdot10^3 & 1.8\cdot10^3\\ \hline \end{array}

n:=12\; f:=0.20 \; Q0:=120

G\alpha(dQ\alpha,P\alpha):=Q0\cdot(1+dQ\alpha)\cdot P\alpha\cdot (1-f)

GS\alpha(Q\alpha,P\alpha):=n\cdot Q0\cdot(1+Q\alpha)\cdot P\alpha\cdot (1-f)

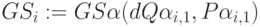GS\alphaL_i:=GS\alpha(dQ\alpha_{i,1},P\alpha_{i,1}), GS\alphaR_i:=GS\alpha(dQ\alpha_{i,2},P\alpha_{i,2})

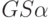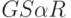Матрица интервалов достоверности прибыли GS\alpha. Левый GS\alpha L и правый GS\alpha R край сечения

GS\alpha L=\begin{array}{|c|c|} \hline & 1 \\ \hline 1 & 1.5\cdot10^6 \\ \hline 2 & 1.6\cdot10^6 \\ \hline 3 & 1.6\cdot10^6\\ \hline 4 & 1.7\cdot10^6\\ \hline 5 & 1.7\cdot10^6 \\ \hline 6 & 1.8\cdot10^6\\ \hline 7 & 1.8\cdot10^6 \\ \hline 8 & 1.9\cdot10^6\\ \hline 9 & 1.9\cdot10^6\\ \hline 10 & 2\cdot10^6\\ \hline 11 & 2.1\cdot10^6\\ \hline \end{array}, GS\alpha R=\begin{array}{|c|c|} \hline & 1 \\ \hline 1 & 2.5\cdot10^6 \\ \hline 2 & 2.4\cdot10^6 \\ \hline 3 & 2.4\cdot10^6\\ \hline 4 & 2.4\cdot10^6\\ \hline 5 & 2.3\cdot10^6 \\ \hline 6 & 2.3\cdot10^6\\ \hline 7 & 2.3\cdot10^6 \\ \hline 8 & 2.2\cdot10^6\\ \hline 9 & 2.2\cdot10^6\\ \hline 10 & 2.2\cdot10^6\\ \hline 11 & 2.1\cdot10^6\\ \hline \end{array}

GS0:=augment(GS\alpha L,\alpha), GS1:=augment(GS\alpha R,\alpha)

GS0=\begin{array}{|c|c|c|} \hline & 1 & 2 \\ \hline 1 & 1.5\cdot10^6 & 0\\ \hline 2 & 1.6\cdot10^6 & 0.1\\ \hline 3 & 1.6\cdot10^6 & 0.2\\ \hline 4 & 1.7\cdot10^6 & 0.3\\ \hline 5 & 1.7\cdot10^6 & 0.4 \\ \hline 6 & 1.8\cdot10^6 & 0.5\\ \hline 7 & 1.8\cdot10^6 & 0.6 \\ \hline 8 & 1.9\cdot10^6 & 0.7\\ \hline 9 & 1.9\cdot10^6 & 0.8\\ \hline 10 & 2\cdot10^6 & 0.9\\ \hline 11 & 2.1\cdot10^6 &amp; 1\\ \hline \end{array}

GS1=\begin{array}{|c|c|c|} \hline &amp; 1 &amp; 2 \\ \hline 1 & 2.5\cdot10^6 & 0 \\ \hline 2 & 2.4\cdot10^6 & 0.1\\ \hline 3 & 2.4\cdot10^6 & 0.2\\ \hline 4 & 2.4\cdot10^6 & 0.3\\ \hline 5 & 2.3\cdot10^6 & 0.4 \\ \hline 6 & 2.3\cdot10^6 & 0.5\\ \hline 7 & 2.3\cdot10^6 & 0.6 \\ \hline 8 & 2.2\cdot10^6 & 0.7\\ \hline 9 & 2.2\cdot10^6 & 0.8\\ \hline 10 & 2.2\cdot10^6 & 0.9\\ \hline 11 & 2.1\cdot10^6 & 1\\ \hline \end{array}

График функции принадлежности нечеткого множества исследуемой прибыли GS

Рис. 6.23. График функции принадлежности нечеткого множества исследуемой прибыли GS

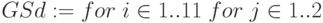
GSd:=for\; i\in 1..11 \; for \; j\in 1..2

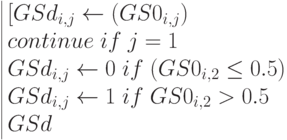\begin{array}{|lc} [GSd_{i,j}\leftarrow (GS0_{i,j}) \\ continue \; if\; j=1 \\ GSd_{i,j}\leftarrow 0 \; if \; (GS0_{i,2}\le 0.5) \\ GSd_{i,j}\leftarrow 1 \; if \; GS0_{i,2}> 0.5 \\ GSd \end{array} , \begin{array}{|lc} [GSd1_{i,j}\leftarrow (GS1_{i,j}) ]\\ continue \; if\; j=1 \\ GSd1_{i,j}\leftarrow 0 \; if \; (GS1_{i,2}\le 0.5) \\ GSd1_{i,j}\leftarrow 1 \; if \; GS1_{i,2}> 0.5 \\ GSd1 \end{array}

GS0=\begin{array}{|c|c|c|} \hline & 1 & 2 \\ \hline 1 & 1.5\cdot10^6 & 0\\ \hline 2 & 1.6\cdot10^6 & 0.1\\ \hline 3 & 1.6\cdot10^6 & 0.2\\ \hline 4 & 1.7\cdot10^6 & 0.3\\ \hline 5 & 1.7\cdot10^6 & 0.4 \\ \hline 6 & 1.8\cdot10^6 & 0.5\\ \hline 7 & 1.8\cdot10^6 & 0.6 \\ \hline 8 & 1.9\cdot10^6 & 0.7\\ \hline 9 & 1.9\cdot10^6 & 0.8\\ \hline 10 & 2\cdot10^6 & 0.9\\ \hline 11 & 2.1\cdot10^6 & 1\\ \hline \end{array}

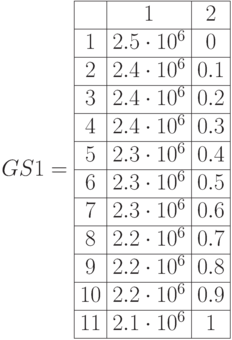
GS1=\begin{array}{|c|c|c|} \hline & 1 & 2 \\ \hline 1 & 2.5\cdot10^6 & 0 \\ \hline 2 & 2.4\cdot10^6 & 0.1\\ \hline 3 & 2.4\cdot10^6 & 0.2\\ \hline 4 & 2.4\cdot10^6 & 0.3\\ \hline 5 & 2.3\cdot10^6 & 0.4 \\ \hline 6 & 2.3\cdot10^6 & 0.5\\ \hline 7 & 2.3\cdot10^6 & 0.6 \\ \hline 8 & 2.2\cdot10^6 & 0.7\\ \hline 9 & 2.2\cdot10^6 & 0.8\\ \hline 10 & 2.2\cdot10^6 & 0.9\\ \hline 11 & 2.1\cdot10^6 & 1\\ \hline \end{array}

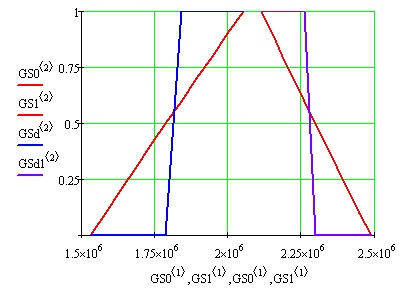
График функции принадлежности нечеткого множества GS0 и GS1 и множества, ближайшего к нечеткому GSd и GSd1

Рис. 6.24. График функции принадлежности нечеткого множества GS0 и GS1 и множества, ближайшего к нечеткому GSd и GSd1

Сравнительные результаты решения методом Монте-Карло и методом нечетких множеств

Достоверные значения прибыли лежат в пределах от 1.8•10^6 до 2.3•10^6 (руб) . Значение прибыли 2.•10^6 также лежит в интервале достоверности. В таблице 6.4 приведены результаты решения этой задачи методом Монте-Карло. Прибыль, рассчитанная вероятностно - статистическим методом лежит в пределах (1.85 – 2.75)\cdot 10^6 (руб) со средним значением 2.22\cdot 10^6 руб

Показатели Среднее значение Среднеквадратичное отклонение Максимальное значение минимальное значение коэффициент вариации
Прибыль фирмы (руб) 2.22\cdot 10^6 0.102\cdot 10^6 2.75\cdot 10^6 1.85\cdot 10^6 4,6\%
Дальше >>
< Лекция 5 || Лекция 6: 123456789

Вопросы и ответы

вопросов: 0