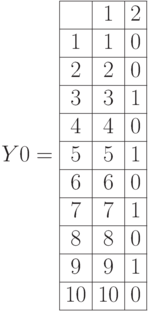Нечеткие множества
6.5 Операции над нечеткими множествами
Рассмотрим операции над нечеткими множествами.
Дополнение. Пересечение. Объединение.
Пусть дано множество 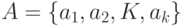 и два его нечетких подмножества:
и два его нечетких подмножества: 
Дополнением нечеткого множества 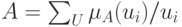 называют множество
называют множество
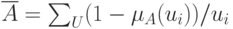 |
( 6.4) |
Пересечением нечетких множеств 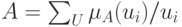 и
и 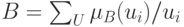 называют нечеткое множество
называют нечеткое множество
 |
( 6.5) |
Объединением нечетких множеств 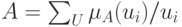 и
и 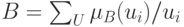 называют нечеткое множество
называют нечеткое множество
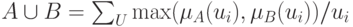 |
( 6.6) |
Продемонстрируем операции над множествами средствами программы MathCad.
Пример 6.5
Приводим листинги операций дополнения, пересечения, объединения для нечетких множеств в виде матриц примера 6.1. (рис.6.7, рис. 6.8):
Дополнения нечетких множеств.  – единичная матрица.
– единичная матрица.
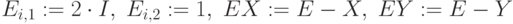
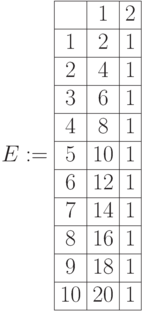 ,
,
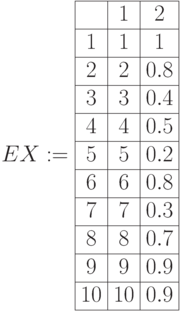 ,
,
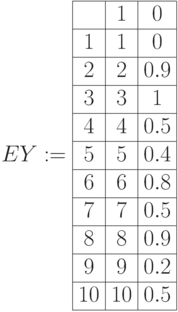
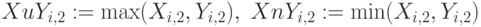
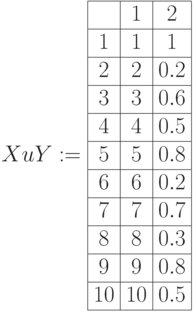 ,
,
Пример 6.6
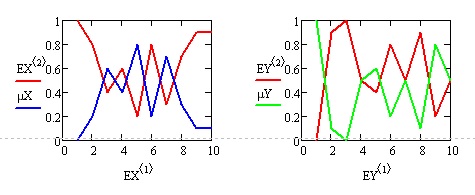
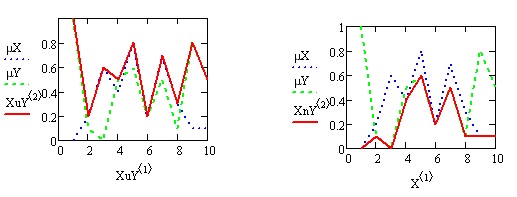
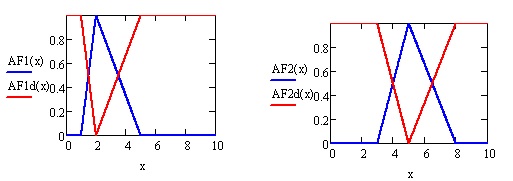
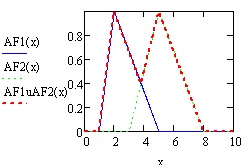
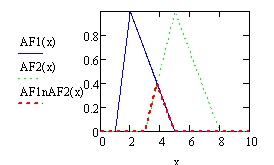
Приводим листинги операций дополнения, пересечения, объединения для нечетких множеств примера 6.2 с треугольными функциями принадлежности. (рис.6.9, рис. 6.10,6.11 )
Дополнение множеств 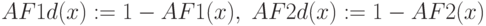
Объединение и пересечение множеств 
Пересечение множеств 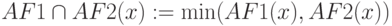
Расстояние между множествами
Чтобы определить расстояние между элементами множества  , надо наложить метрику на это множество. Рассмотрим следующие метрики. Математическим прообразом реального трехмерного пространства является пространство Евклида. Пространство Евклида обозначают обычно
, надо наложить метрику на это множество. Рассмотрим следующие метрики. Математическим прообразом реального трехмерного пространства является пространство Евклида. Пространство Евклида обозначают обычно 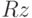 . Для линейных дискретных пространств, особенностью которых является то, что координаты векторов могут принимать лишь дискретные значения, известно пространство Хемминга. Если рассмотреть функции принадлежности всех множеств на универсальном множестве
. Для линейных дискретных пространств, особенностью которых является то, что координаты векторов могут принимать лишь дискретные значения, известно пространство Хемминга. Если рассмотреть функции принадлежности всех множеств на универсальном множестве  , то они образуют функциональное множество всех функций, определенных на
, то они образуют функциональное множество всех функций, определенных на  , и принимающих значения на отрезке
, и принимающих значения на отрезке ![[0, 1]](/sites/default/files/tex_cache/264884439b70ab09a86bc848421c6de6.png) . Метрика на множестве
. Метрика на множестве  — это функция
— это функция 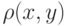 , сопоставляющая каждой паре элементов
, сопоставляющая каждой паре элементов  действительное число по правилу выбранного пространства.
действительное число по правилу выбранного пространства.
Чтобы найти расстояние между множествами  и
и  используются метрики, представленные в таблице 6.2:
используются метрики, представленные в таблице 6.2:
| Вид метрики | Вид множества | |
 – дискретное множество, – дискретное множество, число его элементов число его элементов |
![U=[a, b]](/sites/default/files/tex_cache/5e6b1be80ee339852dd9af4eb73c6660.png) — непрерывное множество — непрерывное множество |
|
| Линейное расстояние (расстояние Хемминга) | 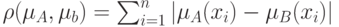 |
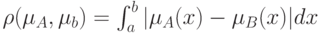 |
| Евклидово расстояние | 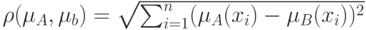 |
 |
Пример. 6.7
Для нечетких множеств  и
и  примера 6.1. построим расстояние между множествами в среде MathCad. Обозначим
примера 6.1. построим расстояние между множествами в среде MathCad. Обозначим  – расстояние по Хеммингу,
– расстояние по Хеммингу,  - расстояние по Евклиду (см. рис. 6.2):
- расстояние по Евклиду (см. рис. 6.2):
 ,
, 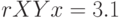
 ,
, 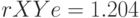
Определение понятия "обычное множество, ближайшее к нечеткому"
Обычным множеством, ближайшим к нечеткому множеству  с функцией принадлежности
с функцией принадлежности 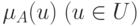 , называют подмножество
, называют подмножество 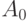 множества
множества  , характеристическая функция которого имеет вид:
, характеристическая функция которого имеет вид:
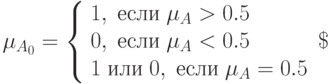 |
( 6.7) |
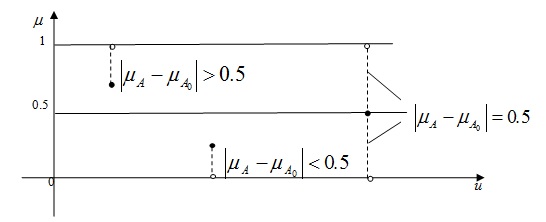
Геометрический смысл понятия "обычное множество 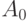 , ближайшее к нечеткому множеству
, ближайшее к нечеткому множеству  " иллюстрирует рис. 6.12.
" иллюстрирует рис. 6.12.
Значения 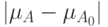 при различном расположении точек графиков функций:
при различном расположении точек графиков функций:
 - функция
- функция 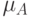 ,
,  - функция
- функция 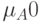
Как видно на рисунке, справедливы неравенства
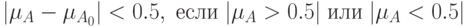
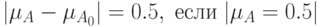 независимо от того
независимо от того 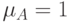 или
или 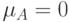
Если  — обычное множество, то оно является ближайшим к самому себе. Это следует непосредственно из определения.
— обычное множество, то оно является ближайшим к самому себе. Это следует непосредственно из определения.
Пример 6.8
Для множеств  и
и  примера 6.1 построим в MathCad множества
примера 6.1 построим в MathCad множества  и
и  – ближайшие к нечетким, воспользуемся встроенной функцией
– ближайшие к нечетким, воспользуемся встроенной функцией
if (условие, результат1, результат2)
результат 1 – если условие выполнено, результат 2 в противном случае.
 – множества ближайшие к нечетким
– множества ближайшие к нечетким  и
и 
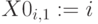 ,
, 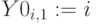
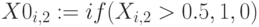 ,
, 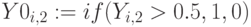
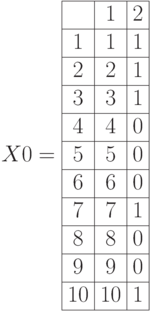 ,
,