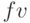Финансово-экономические модели
Задача 2.1.
Облигация номиналом 500 тыс. руб. выпущена на 5 лет при номинальной (годовой) ставке процента 10 %. Держатель облигации будет капитализировать проценты. Определить будущую стоимость при начислении процентов: один раз в год, один раз в полугодие, раз в квартал, ежемесячно. Для каждого варианта определить эффективную ставку процента.
Решение (рис.2.1).
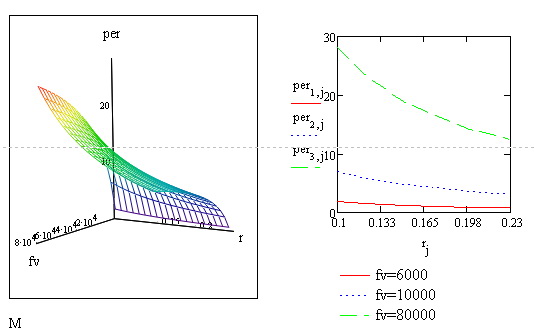
Количество начислений в году m вводим в виде вектора. При расчете используем формулу (2.3) и альтернативно встроенные финансовые функции 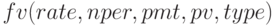 – будущая сумма и
– будущая сумма и 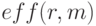 эффективная ставка. Рассчитанные финансовые величины
эффективная ставка. Рассчитанные финансовые величины 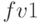 будущую стоимость и
будущую стоимость и 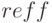 эффективную ставку также имеем в виде векторов. Все финансовые функции при расчетах учитывают движение денег: если в начале срока сумма
эффективную ставку также имеем в виде векторов. Все финансовые функции при расчетах учитывают движение денег: если в начале срока сумма 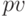 вносится – отрицательна, тогда будущая сумма
вносится – отрицательна, тогда будущая сумма 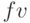 после начисления процентов будет получена – положительна.
после начисления процентов будет получена – положительна.

Входные данные:
 ,
,  ,
,  ,
, 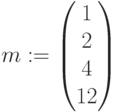
Количество начислений в году. Решение:
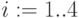
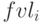 – будущая стоимость,
– будущая стоимость, 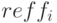 – эффективная ставка для начисления
– эффективная ставка для начисления  раз в год
раз в год
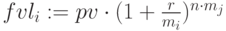 ,
, 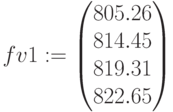 ,
, 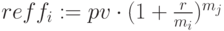 ,
, 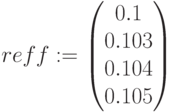
Используем встроенные функции 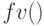 и
и 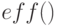 – эффективная ставка
– эффективная ставка
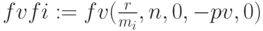 ,
, 
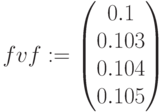 ,
, 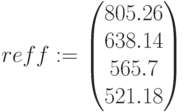
 – будущая сумма от числа начислений процентов в году,
– будущая сумма от числа начислений процентов в году, 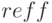 – будущая сумма от эффективной ставки
– будущая сумма от эффективной ставки
Задача 2.2.
Вклад 50000 руб.помещен в банк. За сколько лет будет накоплена сумма в 60000 руб., 100000 руб, 800000 руб., если годовая ставка равна 10%, 12%,15%,20%, 25%. Рассчитать варианты. Проценты начисляются один раз в квартал.
Решение (рис.2.2).
Данные: 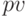 , процентную ставку
, процентную ставку  вводим как векторы. Количество периодов –
вводим как векторы. Количество периодов – 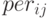 – матрица:
– матрица:  —количество накопленных сумм,
—количество накопленных сумм,  – количество ставок. Расчет выполнен по формуле (2.12). Выбирая для расчета финансовую функцию, следует сказать, что в Mathcad введены разные функции для расчета элементарного потока и для периодического потока, в отличие от пакета русских функций (например, в пакете MS Excel), в котором функция одна –
– количество ставок. Расчет выполнен по формуле (2.12). Выбирая для расчета финансовую функцию, следует сказать, что в Mathcad введены разные функции для расчета элементарного потока и для периодического потока, в отличие от пакета русских функций (например, в пакете MS Excel), в котором функция одна –  . Функция
. Функция  возвращает число составных периодов, необходимых для получения будущего значения вклада при заданных текущем значении вклада и проценте начислений, при этом
возвращает число составных периодов, необходимых для получения будущего значения вклада при заданных текущем значении вклада и проценте начислений, при этом 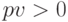 ,
, 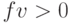 . Функция
. Функция  возвращает число периодов для вклада или займа, основанных на периодичности, постоянных платежах, использующих фиксированную процентную ставку, и особое текущее значение. Эту функцию рассмотрим позже. В данной задаче выбираем функцию
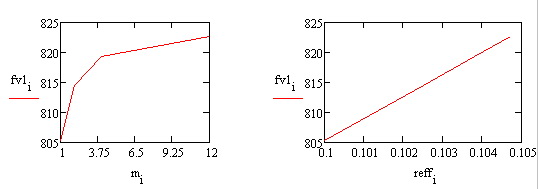
возвращает число периодов для вклада или займа, основанных на периодичности, постоянных платежах, использующих фиксированную процентную ставку, и особое текущее значение. Эту функцию рассмотрим позже. В данной задаче выбираем функцию 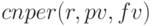 . На рисунке 2.2 показан графики зависимости срока накопления от будущей суммы и ставки.
. На рисунке 2.2 показан графики зависимости срока накопления от будущей суммы и ставки.
Расчет срока накопления.
Входные данные
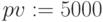 ,
, 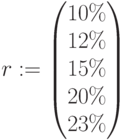 ,
, 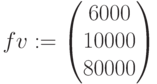 ,
, 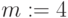
Решение:
 ,
,  ,
, 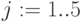
Срок погашения – количество периодов 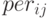 для
для 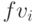 и
и 
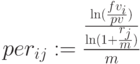
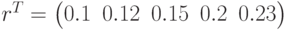
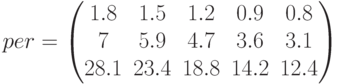
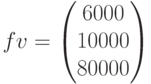
Применим финансовую функцию:
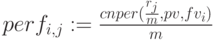
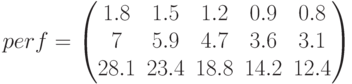
Простроение графиков срока накопления от будущей стоимости и ставки
Построим график 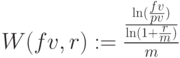 ,
, 
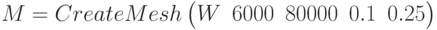 - срок накопления от ставки
- срок накопления от ставки  и накопленной суммы
и накопленной суммы