НОУ ИНТУИТ | Введение в Octave. Лекция 10: Решение оптимизационных задач

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Пример 10.10. Для изготовления четырёх видов изделий используется токарное, фрезерное, сверлильное, расточное шлифовального оборудование, а также комплектующие изделия. Сборка изделий требует сборочно-наладочных работ. В таблице 10.4 представлены: нормы затрат ресурсов на изготовление различных изделий, наличие каждого из ресурсов, прибыль от реализации одного изделия, ограничения на выпуск изделий второго и третьего типа [1]. Сформировать план выпуска продукции для достижения максимальной прибыли.

Таблица 10.4. Нормы затрат ресурсов к примеру 10.10
Ресурсы	Нормы затрат на одно изделие				Общий объём ресурсов
Производительность оборудования (человеко-ч)
токарного	550		620		64270
фрезерного	40	30	20	20	4800
сверлильного	86	110	150	52	22360
расточного	160	92	158	128	26240
шлифовального		158	30	50	7900
Комплектующие изделия (шт.)	3	4	3	3	520
Сборочно-наладочные работы (человеко-ч)	4.5	4.5	4.5	4.5	720
Прибыль от реализации одного изделия (тыс. руб.)	315	278	573	370
Выпуск
минимальный		40
максимальный			120

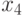Пусть x_1 — количество изделий первого вида, x_2 — количество изделий второго вида, x_3 и x_4 — количество изделий третьего и четвёртого вида соответственно. Тогда прибыль от реализации всех изделий вычисляется по формуле

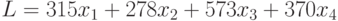$L=315x_{1}+278x_{2}+573x_{3}+370x_{4}$

( 10.12)

Ограничения на фонд рабочего времени формируют следующие ограничения

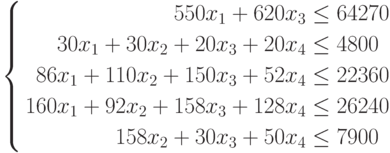$\left\{ \begin{aligned} 550x_{1}+620x_{3}&\le 64270\\ 30x_{1}+30x_{2}+20x_{3}+20x_{4}&\le 4800\\ 86x_{1}+110x_{2}+150x_{3}+52x_{4}&\le 22360\\ 160x_{1}+92x_{2}+158x_{3}+128x_{4}&\le 26240\\ 158x_{2}+30x_{3}+50x_{4}&\le 7900 \end{aligned} \right.$

( 10.13)

Ограничение на возможное использование комплектующих изделий

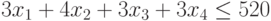$3x_{1}+4x_{2}+3x_{3}+3x_{4}\le 520$

( 10.14)

Ограничение на выполнение сборочно-наладочных работ

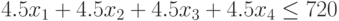$4.5x_{1}+4.5x_{2}+4.5x_{3}+4.5x_{4}\le 720$

( 10.15)

Ограничения на возможный выпуск изделий каждого вида

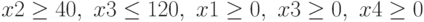$x2\ge 40,\ x3\le 120,\ x1\ge 0,\ x3\ge 0,\ x4\ge 0$

( 10.16)

Сформулируем задачу линейного программирования.

Найти значения $x_{1},x_{2},x_{3}$ и

$x_{4}$

при которых функция цели

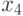
(10.12) достигает своего максимального значения и выполняются ограничения (10.13)–(10.16).

Рассматриваемая задача из широко известной книги [1] была интересна авторам в связи с тем, что ещё 25 лет назад для решения задач подобной сложности использовали большие ЭВМ и специализированные пакеты решения оптимизационных задач. На подготовку данные и решение её затрачивался не один час. Мы же попробуем решить её в Octave и посмотрим сколько времени у нас на это уйдёт.

Сформируем параметры функции gplk :

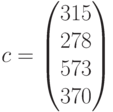$c=\begin{pmatrix}315\\278\\573\\370\end{pmatrix}$ — коэффициенты при неизвестных функции цели,

$a=\begin{pmatrix} 550&0&620&0\\ 40&30&20&20\\ 86&110&150&52\\ 160&92&158&128\\ 0&158&30&50\\ 3&4&3&3\\ 4.5&4.5&4.5&4.5\\ 0&1&0&0\\ 0&0&1&0\\ 1&0&0&0\\ 871 0&0&1&0\\ 872 0&0&0&1 873 \end{pmatrix}$ — матрица системы ограничений (четыре переменных и двенадцать ограничений),

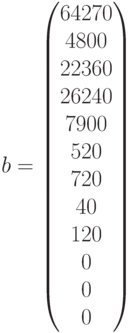$b=\begin{pmatrix}64270\\4800\\22360\\26240\\7900\\520\\720\\40\\120\\0\\0\\0\end{pmatrix}$ — свободные члены системы ограничений,

ctype ="UUUUUUULULLL" — массив символов, определяющий тип ограничения^{9Первые три ограничения типа "меньше", четвёртое и пятое — типа "равно".},

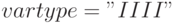vartype ="IIII" — массив, определяющий тип переменной, в данном случае все переменные целые (задача целочисленного программирования),

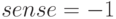sense = -1 — задача на максимум.

Программа решения задачи в Octave представлена в листинге 10.13.

	
c = [315; 278; 573; 370];
a =[550 0 620 0; 40 30 20 20; 86 110 150 52; 160 92 158 128; 0 158
	30 50; 3 4 3 3; 4.5 4.5 4.5 4.5; 0 1 0 0; 0 0 1 0; 1 0 0 0; 0 0
	1 0; 0 0 0 1];
b = [64270; 4800; 22360; 26240; 7900; 520; 720; 40; 120; 0; 0; 0];
ctype="UUUUUUULULLL"; vartype= "IIII"; sense =-1;
[xmax, fmax, status]= glpk(c, a, b, [ ], [ ], ctype, vartype, sense)
% Результаты решения
[xmax, fmax, status]= glpk(c, a, b, [ ], [ ], ctype, vartype, sense)
xmax =
	65
	40
	46
	4
fmax = 59433
status = 171

Листинг 10.13. Решение задачи из примера 10.10

Для получения максимальной прибыли (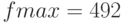 fmax = 492 ) необходимо произвести 65 единиц изделий первого типа, 40 — второго, 46 — третьего - и 4 — четвёртого. Значение параметра 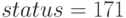status = 171 говорит о корректности решения задачи линейного программирования.

Для написания программы и решения довольно сложной задачи в Octave понадобилось буквально пару минут.

Подобным образом можно решать всевозможные задачи линейного программирования. Кроме Octave, для решения задач линейного программирования авторы использовали электронные таблицы OpenOffice.org Calc, MS Office Excel, математические программы MathCad, Matlab, Maple, Mathematica, Scilab. На наш взгляд, именно Octave, обладает самой гибкой и мощной функцией gplk для решения задач линейного программирования из всех свободных и проприетарных программ.

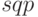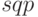Рассмотренных двух функций ( gplk и sqp ) достаточно для решения очень многих оптимизационных задач. Если читателю встретятся оптимизационные задачи, которые невозможно решить с помощью gplk и sqp , то авторы рекомендуют ему обратиться к пакету расширений Minimization для GNU Octave. Краткое описание функций этого пакета на английском языке с некоторыми примерами приведено на странице http://octave.sourceforge.net/optim/overview.html.

Дальше >>

Авторизоваться

Введение в Octave

Решение оптимизационных задач

Вопросы и ответы