Решение оптимизационных задач

Пример 10.9. Для изготовления трёх видов изделий (А, Б, В) используется токарное, фрезерное, шлифовальное и сварочное оборудование. Затраты времени на обработку одного изделия каждого типа представлены в таблице 10.3. Общий фонд рабочего времени каждого вида оборудования и прибыль от реализации изделий каждого типа представлены этой же таблице. Составить план выпуска изделий для достижения максимальной прибыли [1].

Пусть — количество изделий вида А, — количество изделий вида Б, — вида В.

Прибыль от реализации всех изделий составляет

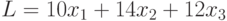( 10.9)

Общий фонд рабочего времени фрезерного оборудования составляет 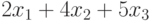. Эта величина не должна превышать 120 часов.

( 10.10)

Запишем аналогичные ограничения для фонда рабочего времени токарного, сварочного, шлифовального оборудования

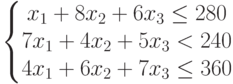( 10.11)

Таким образом получаем следующую задачу линейного программирования.

Найти такие положительные значения 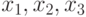при которых функция цели (10.9) достигает максимального значения и выполняются ограничения (10.10)–(10.11).

Теперь решим эту задачу в Octave с помощью функции .

Сформируем параметры функции :

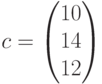— коэффициенты при неизвестных функции цели,

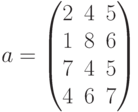— матрица системы ограничений (три переменных и четыре ограничений),

–– свободные члены системы ограничений,

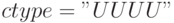— массив, определяющий тип ограничения^{8Все четыре ограничения типа "меньше".},

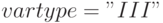— массив, определяющий тип переменной, в данном случае все переменные целые,

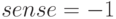— задача на максимум.

Решение задачи в Octave представлено в листинге 10.12

	
c = [10; 14; 12]; a =[2 4 5; 1 8 6; 7 4 5; 4 6 7]; b = [ 1 2 0; 2 8 0; 2 4 0; 3 6 0];
ctype="UUUU"; vartype= "III"; sense =-1;
[xmax, fmax, status] =glpk(c, a, b, [0;0;0], [], ctype, vartype, sense)
% Результаты решения
xmax =
	24
	18
	0
fmax = 492
status = 171

Таким образом для получения максимальной прибыли (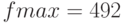) необходимо произвести 24 единицы изделия типа А и 18 единиц изделия типа Б. Значение параметра 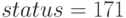говорит о корректности решения задачи линейного программирования.