Решение оптимизационных задач

Пример 10.2. Найти минимум функции Розенброка^{1В классическом определении функции Розенброка N = 100 (N > 0, достаточно большое число), авторы используют N=20. (Прим. редактора.)}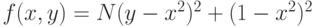

На рис. 10.1 изображен график функции:

Построим график функции Розенброка для (см. листинг 10.2). График полученной поверхности приведён на рис. 10.2.

	
[x y]= meshgrid(-2:0.1:2, 2:-0.1:-2);
z =20*(y-x.^2).^2+(1-x).^2;
surf(x, y, z);

Как известно, функция Розенброка имеет минимум в точке (1,1) равный 0. В виду своей специфики функция Розенброка является тестовой для алгоритмов минимизации. Найдём минимум этой функции с помощью функции 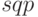(см. листинг 10.3).

При решении задач на экстремум функций многих переменных следует учитывать особенности синтаксиса при определении оптимизируемой функции. Аргументом функции многих переменных (в нашем случае — её имя ) является массив , первая переменная имеет имя 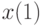, вторая 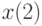и т. д. Если имя аргумента функции многих переменных будет другим — допустим m, то изменятся и имена переменных: 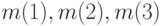и т.д.

	
function y=r(x)
	y=20*(x(2)-x(1)^2)^2+(1-x(1))^2;
endfunction
x0 = [0; 0];
[x, obj, info, iter]= sqp(x0, @r)
% Результаты вычислений
x =
	1.00000
	1.00000
obj = 7.1675e-13
info = 101
iter = 14

Рис. 10.2. График функции Розенброка

Как и следовало ожидать, функция 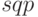нашла минимум в точке (1,1), само значение 0 найдено достаточно точно (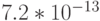). Значение info = 101 говорит о корректном решении задачи, для нахождения минимального значения функции Розенброка потребовалось 14 итераций.

Таким образом, функция 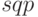предназначена для поиска минимума функций (как одной, так и нескольких переменных) с различными ограничениями.

Рассмотрим несколько задач поиска экстремума с ограничениями

Пример 10.3. Найти максимум и минимум функции ([1])

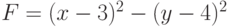при ограничениях: .

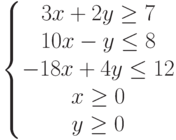В функции 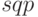все ограничения должны быть вида 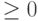. Поэтому второе и третье ограничение умножим на -1, и перенесём всё в левую часть неравенств. В результате этих несложных преобразований система ограничений примет вид:

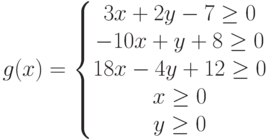
Последовательно рассмотрим задачу на минимум (листинг 10.4) и максимум (листинг 10.5).

	
% В задаче на минимум функция, в которой хранится F(x) будет такой
function y=f(x)
	y=(x(1)-3)^2+(x(2)-4)^2;
endfunction
% Вектор-функцию ограничений g(x) можно записать так:
function r = g(x)
	r=[3*x(1)+3*x(2)-7; -10*x(1)+x(2)+8;18*x(1)-4*x(2)+12;x(1);x(2)];
endfunction
% Вычисляем с помощью функции sqp
x0 = [0; 0]; [x, obj, info, iter]= sqp(x0, @f, [ ], @g)
minimum=f(x)
% Результаты
x =
	1.2178
	4.1782
obj = 3.2079
info = 101
iter = 5
mininum =3.2079

Минимум 3.2079 достигается в точке (1.2178, 4.1782), значение info = 101 говорит о корректном решении задачи, для нахождения минимального значения потребовалось всего 5 итераций.

Теперь рассмотрим решение задачи на максимум. Функция 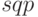может искать только минимум. Поэтому вспомним, как задача на максимум сводится к задаче на минимум: 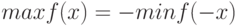. Это учтено в листинге 10.5.

	
function y=f(x)
	y=(x(1)-3)^2+(x(2)-4)^2;
endfunction
% Определяем функцию, для которой минимум будет максимумом функции f
function y=f1(x)
y= -f(-x);
endfunction
function r = g(x)
	r=[3*x(1)+2*x(2)-7; -10*x(1)+x(2)+8;18*x(1)-4*x(2)+12;x(1);x(2)];
endfunction
x0 = [0; 0]; [x, obj, info, iter]= sqp(x0, @f1, [ ], @g)
maximum=f(x)
% Результаты работы программы
x =
	2.0000
	12.0000
obj = -281.00
info = 101
iter = 3
maximum = 65.000

Максимум достигается в точке (2,12), его величина равна 65.