|
Возможна ли разработка приложения на Octave с GUI? |
Решение оптимизационных задач
Пример 10.8. Туристическая фирма заключила контракт с двумя турбазами на одном из черноморских курортов, рассчитанных соответственно на 195 и 165 человек. Туристам для посещения предлагается дельфинарий в городе, ботанический сад и походы в горы.
| Турбаза | Дельфинарий | Ботанический сад | Поход в горы |
| 1 | 5 | 9 | 20 |
| 2 | 10 | 12 | 24 |
Составить маршрут движения туристов так, чтобы это обошлось возможно дешевле, если дельфинарий принимает в день 90 организованных туристов, ботанический сад — 170, а в горы в один день могут пойти 105 человек.
Стоимость одного посещения выражается таблицей 10.2.
Для решения задачи введём следующие обозначения:
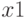 — число туристов первой турбазы, посещающих дельфинарий;
— число туристов первой турбазы, посещающих дельфинарий;
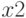 — число туристов первой турбазы, посещающих ботанический сад;
— число туристов первой турбазы, посещающих ботанический сад;
 — число туристов первой турбазы, отправляющихся в поход;
— число туристов первой турбазы, отправляющихся в поход;
 — число туристов второй турбазы, посещающих дельфинарий;
— число туристов второй турбазы, посещающих дельфинарий;
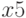 — число туристов второй турбазы, посещающих ботанический сад;
— число туристов второй турбазы, посещающих ботанический сад;
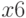 — число туристов второй турбазы, отправляющихся в поход.
— число туристов второй турбазы, отправляющихся в поход.
Составим функцию цели, заключающуюся в минимизации стоимости мероприятий фирмы: Z = 5x1 + 9x2 + 20x3 + 10x4 + 12x5 + 24x6.
Руководствуясь условием задачи, определим ограничения:
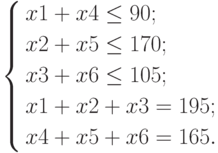
Количество туристов, участвующих в мероприятиях не может быть отрицательным: 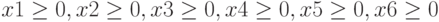 .
.
Кроме того, необходимо помнить, что это задача целочисленного программирования (количество туристов — число целое!!!).
В массиве x будут хранится значения x1, x2, x3, x4, x5 и x6.
Сформируем параметры функции  :
:
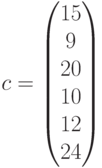 — коэффициенты при неизвестных функции цели,
— коэффициенты при неизвестных функции цели,
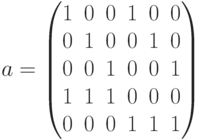 –– матрица системы ограничений шесть переменных и пять ограничений,
–– матрица системы ограничений шесть переменных и пять ограничений,
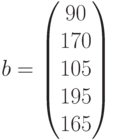 — свободные члены системы ограничений,
— свободные члены системы ограничений,
 — массив, определяющий тип
ограничения7Первые три ограничения типа "меньше", четвёртое и пятое — типа "равно".,
— массив, определяющий тип
ограничения7Первые три ограничения типа "меньше", четвёртое и пятое — типа "равно".,
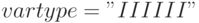 — массив, определяющий тип переменной, в данном случае все переменные целые (задача целочисленного программирования),
— массив, определяющий тип переменной, в данном случае все переменные целые (задача целочисленного программирования),
 — задача на минимум.
— задача на минимум.
Решение задачи представлено в листинге 10.11.
c = [5; 9; 20; 10; 12; 24]; a =[1 0 0 1 0 0;0 1 0 0 1 0;0 0 1 0 0 1;1 1 1 0 0 0;0 0 0 1 1 1]; b = [90; 170; 105; 195; 165]; ctype="UUUSS"; vartype= "IIIIII"; sense =1; [xmin, fmin, status]= glpk(c, a, b, [ ], [], ctype, vartype, sense) % Результаты решения xmin = 90 5 100 0 165 0 fmin = 4475 status = 171Листинг 10.11. Решение задачи из примера 10.8
Значение переменной 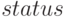 = 171 свидетельствует о корректном решении задачи целочисленного программирования.
= 171 свидетельствует о корректном решении задачи целочисленного программирования.
В результате получилось следующее решение: 90 туристов первой турбазы посетят дельфинарий, 5 туристов первой турбазы и все 165 второй турбазы поедут в ботанический сад, 100 туристов первой турбазы отправятся в поход. Стоимость мероприятия составит 4475.
