Квантовые вычисления
[+]
Опубликован: 03.06.2019 | Доступ: свободный | Студентов: 505 / 76 | Длительность: 09:11:00
Темы: Программирование, Математика, Физика, Суперкомпьютерные технологии
Лекция 18:

Квантовое преобразование Фурье
A
|
версия для печати
< Лекция 17 || Лекция 18: 12 || Лекция 19 >
Ключевые слова: RAND, операции, бит, значение, матрица, вектор, представление, коэффициенты

При обсуждении квантовой реализации классических вычислений, мы ввели несколько стандартных трансформаций, действующих на пространстве кубитов. Эти квантовые элементы RAND, RОR, NОТ и СNОТ представляют трансформации специального вида - все они просто переставляют базисные вектора. Чтобы добиться полной мощности квантового компьютера, необходимо сделать следующий шаг и ввести более общие операции в пространстве 1- и 2-кубита.

Первая трансформация, которую мы введем, называется трансформацией Адамара. Она действует в пространстве 1-кубита и определена следующим образом:

H|0\rangle = \frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle,\\ H|1\rangle=\frac{1}{\sqrt2}|0\rangle-\frac{1}{\sqrt2}|1\rangle

Второе стандартное семейство квантовых элементов - это трансформации поворотов 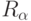R_{\alpha} в пространстве 1 -кубита:

R_{\alpha}|0\rangle=\cos \alpha |0\rangle - \sin \alpha |1\rangle,\\ R_{\alpha}|0\rangle = \sin \alpha |0\rangle+\cos \alpha |1\rangle

Трансформация Адамара и семейство поворотов образуют ортогональную группу О(2) - каждая ортогональная трансформация в пространстве 1 -кубита является либо поворотом, либо произведением поворота и трансформации Адамара.

Последней стандартной квантовой трансформацией является семейство управляемых поворотов 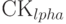СК_{\аlpha}. Это семейство действует в пространстве 2-кубита и определено следующим образом:

CR_{\alpha}|xy\rangle=\begin{cases} |xy\rangle&\text{если} х=0,\\ |x\rangle R_{\alpha}|y\rangle \text{если} x=1 \end{cases}

Поворот применяется ко второму квантовому биту, но это поворот, управляемый значением первого квантового бита. Если первый бит имеет значение 1, поворот применяется, если 0- не применяется.

В стандартном базисе 2-кубит пространства \{ |00 \rangle , |01 \rangle , |10 \rangle , |11 \rangle \} матрица этой трансформации имеет вид:

CR_{\alpha}= \begin{pmatrix}1&0&0&0\\0&1&0&0 \\0&0&\cos \alpha& \sin \alpha \\ 0&0&-\sin \alpha& \cos \alpha\end{pmatrix}

Перейдем к определению квантового преобразования Фурье (КПФ).

В классическом ДПФ входом является вектор измерений (F_0,F_1,\dots,f_{n-1}), выходом - вектор коэффициентов Фурье (a_0,a_1,\dots,a_{n/2-1}, b_0, b_1,\dots b_{M/2-1}) . КПФ делает аналогичную вещь, - только входом и выходом являются п-кубиты:

\sum_{k=0}^{2^n-1}f_k|k_{n-1}\dotsk_1k_0 \rangle \to \sum_{p=0}^{2^{n-1}-1}a_p|p_0p_1\dotsp_{n-2} \rangle|0 \rangle+\sum_{p=0}^{2^{n-1}-1}b_p|p_0p_1\dotsp_{n-2} \rangle|1 \rangle

Здесь k_{n_1}\dots k_1k_0 - бинарное представление целого k. Справа от стрелки удобнее писать биты р в обратном порядке: р = р_{n_2}2^{n-2} + \dots + 2р_1 + р_0, представленных как |р_0р_1 \dots p_{n-2} \rangle. Так как а_р коэффициенты пишутся первыми в последовательности преобразования Фурье, то значение ведущего бита для них равно 0, а для коэффициентов b_p -1.

Цель этой главы представить реализацию КПФ, используя стандартные 1-кубит и 2-кубит операции.

Эта реализация построена на идеях БПФ. Также как БПФ, КПФ является рекурсивным алгоритмом. Это означает, что мы будем использовать КПФ для (n - 1)-кубита при построении КПФ для n-кубитов.

Перечислим вначале 6 шагов реализации КПФ, а затем обсудим каждый шаг в деталях. Замечательное свойство КПФ в том, что оно не требует никакой дополнительной памяти.

Квантовое преобразование Фурье:

Шаг 1. Применить КПФ к первым n - 1 битам входа из n кубитов.

Шаг 2. Применить трансформацию Адамара к последнему биту входа.

Шаг З. Применить СNOТ к последнему биту, управляемую предпоследним битом.

Шаг 4. Применить к предпоследнему биту последовательность поворотов, управляемых предыдущими битами.

Шаг 5. Применить СNОТ к предпоследнему биту, управляемую последним битом.

Шаг 6. Применить СNOТ к первым n - 2 битам, управляемую предпоследним битом.

Начнем со входа, заданного п-кубитом:

\sum_{k=0}^{2^n-1}f_k|k_{n-1}\dots k_1k_0 \rangle

Далее, следуя идеям БПФ, расщепим последовательность f на две последовательности g и h, соответствующие для g четным значениям k, для h -нечетным. После этих изменений в нотации наш входной кубит записывается так:

\sum_{s=0}^{2^{n-1}-1}g_s|s_{n-2}\dots s_0 \rangle|0 \rangle+h_s|s_{n-2} \dots s_0 \rangle|1 \rangle

Выполним Шаг 1 нашей процедуры, применяя КПФ к левым n -1 битам. Результат этой операции таков:

\sum_{s=0}^{2^{n-1}-1}a_p^g|p_0\dots p_{n-3} \rangle|00 \rangle+b_p^g|p_0 \dots p_{n-3} \rangle|10 \rangle+a_p^h|p_0\dotsp_{n-3} \rangle|01 \rangle+b_p^h|p_0\dotsp_{n-3} \rangle|11 \rangle
Дальше >>
< Лекция 17 || Лекция 18: 12 || Лекция 19 >

Вопросы и ответы

вопросов: 0