Криптосистема 1SА
В лекции 3 мы обсуждали криптосистемы, основанные на разделяемом секретном ключе. Для современных приложений Интернет коммерции такие системы непрактичны, так как две стороны, осуществляющие транзакцию, не имеют предварительных контактов. Все же использование шифрования -основа Интернет коммерции, поскольку глобальные сети организованы так, что передаваемые сообщения проходят через цепь серверов, владельцами которых являются сторонние лица, и предсказать точный путь прохождения сообщения не представляется возможным.
Решение проблемы возможно при использовании открытого ключа шифрования. Открытый ключ криптосистемы позволяет каждому зашифровать сообщение, но только тот, кому предназначено сообщение, способен расшифровать его. Представьте себе, что Боб, владелец интернет магазина, желает получить номера кредитных карт своих покупателей, при этом они должны оставаться секретными и недоступными никому кроме Боба. Для этого Боб генерирует два ключа: открытый ключ, который необходим для шифрования, и секретный ключ, необходимый для дешифрования зашифрованного сообщения. Открытый ключ известен каждому, обычно он встроен в Web страницу магазина Боба. Алиса, клиент магазина, использует открытый ключ Боба для шифрования номера своей кредитной карты. Зашифрованный номер она посылает Бобу, чтобы оплатить сделанные ею покупки. Обычно шифрование вьшолняется браузером Алисы, которому известно, как прочесть открытый ключ Боба с его страницы. Браузер запрограммирован на выполнение алгоритма шифрования.
Боб, получив зашифрованное послание от Алисы, расшифрует номер кредитной карты, используя секретный ключ. Так как только Боб имеет секретный ключ, то он единственный, кто способен расшифровать сообщение Алисы.
Одна из первых криптосистем с открытым ключом была предложена в 1974 году Ривестом (Rivest), Шамиром (Shamir), Адлеманом (Adleman). Эта система, известная как RSА (по первым буквам фамилий авторов) основана на факторизации целых - разложения целого числа на множители. Если взять два больших целых числа р и q, то достаточно просто получить их произведение N = рq Однако, если нам дано N и сказано, что оно является произведением двух простых чисел, то найти сомножители - вычислительно трудная задача. Открытый ключ в RSA криптосистеме - это пара целых, N и k, где k - целое со свойством НОД(k, (р - 1) (q - 1)) = 1. Например, можно выбрать k как простое число в интервале: mах(р -1, q -1)<k<(р-1)(q-1).
Секретным ключом являются числа: р, q, s, где s вычисляется как:

Как мы позже покажем, любые оцифрованные данные могут быть представлены последовательностью остатков по модулю 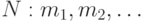 . Алиса каждый остаток m, представляющий простой текст, шифрует, получая остаток с, представляющий зашифрованный текст, используя следующую формулу:
. Алиса каждый остаток m, представляющий простой текст, шифрует, получая остаток с, представляющий зашифрованный текст, используя следующую формулу:

Зашифрованный текст, в виде последовательности 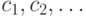 , Алиса посылает Бобу
, Алиса посылает Бобу
Для расшифровки послания Боб вычислит  . Давайте проверим, что в этом случае Боб получит блок т, представляющий простой текст.
. Давайте проверим, что в этом случае Боб получит блок т, представляющий простой текст.
В самом деле, так как ks = 1 mod (р-1)(q-1), то ks = 1+r(р-1)(q-1) для некоторого целого r. Затем, вычисляя по модулю N, получим:

При доказательстве использовался аналог малой теоремы Ферма об остатках по модулю N = pq:
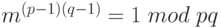
Можно показать, что последняя формула справедлива только тогда, когда НОД(m, pq)= 1. На практике мы исходим из того факта, что для больших простых чисел р, q вероятность того, что указанное равенство не выполняется, настолько мала, что его можно просто игнорировать. Фактически, найти не нулевой остаток m такой, что 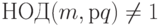 означает выполнить факторизацию рq, поскольку остаток равен либо р, либо q. Так как мы исходим из того, что практически выполнить факторизацию невозможно за разумное время, мы можем также предполагать, что случайная ошибка в схеме шифрования не встретится.
означает выполнить факторизацию рq, поскольку остаток равен либо р, либо q. Так как мы исходим из того, что практически выполнить факторизацию невозможно за разумное время, мы можем также предполагать, что случайная ошибка в схеме шифрования не встретится.
Если кто-то сумеет факторизовать N и найти р и q, тогда он сумеет вычислить произведение (р - 1) (q - 1) и секретный ключ
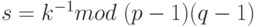
Утверждение. Пусть N - произведение двух неизвестных простых чисел: N = рq. Пусть  - мультипликативная группа обратимых остатков по модулю N. Знание значения порядка М = (р - 1)(q - 1) этой группы позволяет эффективно факторизовать N.
- мультипликативная группа обратимых остатков по модулю N. Знание значения порядка М = (р - 1)(q - 1) этой группы позволяет эффективно факторизовать N.
Доказательство. Прежде всего заметим, что М = (р - 1)(q - 1) = N - р - q + 1, так что если мы знаем N и М, то мы также знаем значение S =р+q=N-М+ 1.
Давайте сконструируем квадратное уравнение, корнями которого являются числа р и q:

Хотя мы не знаем корней, но мы знаем значения коэффициентов квадратичного полинома с нужными нам корнями. Применяя стандартные формулы для корней квадратного уравнения:

найдем значения множителей N - р и q.
Давайте обсудим детали реализации криптосистемы RSА. Прежде всего, как преобразовать произвольные данные в последовательность остатков? Любые оцифрованные данные хранятся в памяти компьютера в виде файла, который можно рассматривать как строку, состоящую из нулей и единиц. Все, что нам нужно сделать, это рассмотреть, как длинные бинарные строки преобразовать в последовательность остатков по модулю N.
Выберем n, такое что 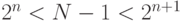 Возьмем теперь нашу длинную бинарную строку и нарежем ее на блоки длины n. Каждый блок теперь может рассматриваться как двоичное число в интервале от 0 до
Возьмем теперь нашу длинную бинарную строку и нарежем ее на блоки длины n. Каждый блок теперь может рассматриваться как двоичное число в интервале от 0 до 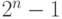 . Добавим 2 к этому числу, так что результат будет между 2 и
. Добавим 2 к этому числу, так что результат будет между 2 и 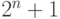 , так что его можно интерпретировать как остаток по модулю N. Двойку мы добавляем для того, чтобы избежать остатков 0 и 1.
, так что его можно интерпретировать как остаток по модулю N. Двойку мы добавляем для того, чтобы избежать остатков 0 и 1.
Еще одна техническая проблема, заслуживающая исследования - это сложность вычисления  . Значение s сравнимо с N, так что может быть очень большим. Давайте зададимся вопросом, как много умножений необходимо выполнить, чтобы вычислить, например,
. Значение s сравнимо с N, так что может быть очень большим. Давайте зададимся вопросом, как много умножений необходимо выполнить, чтобы вычислить, например,  . С первого взгляда - 2017, но фактически это можно сделать намного эффективнее. Давайте представим 2018 в виде разложения по степеням числа 2:
. С первого взгляда - 2017, но фактически это можно сделать намного эффективнее. Давайте представим 2018 в виде разложения по степеням числа 2:
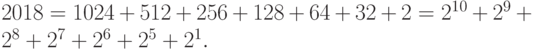
Для возведения числа в квадрат требуется одно умножение. Повторяя возведение в квадрат, можно вычислить: 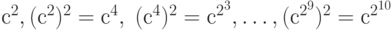 . Вычисления потребуют 10 умножений. Затем мы используем разложение числа 2018, чтобы выразить:
. Вычисления потребуют 10 умножений. Затем мы используем разложение числа 2018, чтобы выразить:
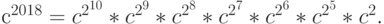
Таким образом потребовалось всего 16 умножений для вычисления  . В общем случае требуется не более
. В общем случае требуется не более  умножений для вычисления
умножений для вычисления 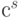 .
.
Еще один возможный источник трудностей - это размер чисел, участвующих в вычислениях. Для больших s число 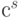 огромное. К счастью нам необходимо вычислить
огромное. К счастью нам необходимо вычислить 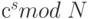 . Если после каждого умножения будем брать остаток по модулю N, то нам не придется иметь дело с целыми, превосходящими
. Если после каждого умножения будем брать остаток по модулю N, то нам не придется иметь дело с целыми, превосходящими 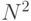 .
.
