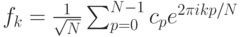За рамками этого курса
Комплексные числа. Общепринятый способ описания квантового состояния использует комплексные, а не вещественные числа. Дадим здесь краткое введение в комплексные числа. Начальной точкой является введение мнимого числа i, которое представляет корень квадратный из минус единицы, мы постулируем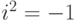 
. Комплексное число записывается в форме а + bi, где а - вещественное число, представляющее вещественную часть комплексного числа, bi - мнимая часть с вещественным числом b. Приведем примеры сложения и умножения комплексных чисел:
Новой операцией над комплексными числами является операция сопряжения, которая меняет знак мнимой части. Операция обычно записывается как надчеркивание комплексного числа:
Сопряжение имеет следующие свойства, справедливые для любой пары комплексных чисел z и w:
У комплексного числа есть аналог абсолютного значения, называемый нормой (модулем):
Норма ненулевого комплексного числа - положительное вещественное число. Существует легко проверяемая связь между комплексно сопряженным числом и нормой:
Это отношение позволяет определить операцию деления для комплексных чисел:
Приведем пример:
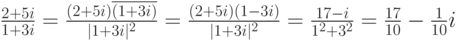
Эрмитово векторное пространство состоит из векторов, чьи компоненты являются комплексными числами. Скалярное произведение в Эрмитовом пространстве определяется следующим образом:
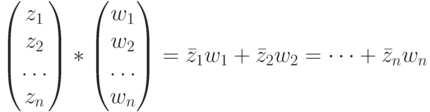
При таком определении скалярное произведение ненулевого комплексного вектора с самим собой является положительным веществеиным числом:
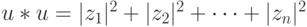
для
Это позволяет определить длину комплексного вектора как 
Кубит является комплексным вектором:
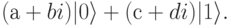
Если при рассмотрении фотона учитывать его поляризацию при поворотах одновременно с линейной поляризацией, то его квантовое состояние моделируется комплексным 1-кубитом.
В общем случае, n-кубит выражается как:
с условием, что длина такого вектора равна 1:
Когда мы выполняем измерение такого n-кубита, вероятность наблюдения значения k равна 
, которая является неотрицательным вещественным числом.
При обсуждении эволюции квантовых состояний в комплексных числах вещественные ортогональные матрицы заменяются матрицами комплексных чисел, удовлетворяющих условию 
Т. Здесь сопряженная матрица состоит из сопряженных элементов. Комплексная матрица, удовлетворяющая этому условию называется унитарной матрицей.
Многие функция могут быть расширены и определены для комплексных чисел. В частности, важным примером является комплексная экспоненциальная функция. Экспонента комплексного числа определена следующей формулой Эйлера:
Комплексная версия дискретного преобразования Фурье основана на комплексной экспоненте. Оказывается, что с комплексной версией ДПФ проще работать, чем с ДПФ для вещественных чисел. Коэффициенты Фурье комплексной последовательности 
вычисляются следующим образом:
Обратное преобразование Фурье восстанавливает исходную последовательность подобным же способом:
