Квантовая телепортация
Два объекта в идентичном квантовом состоянии физически не отличимы друг от друга. Идея квантовой телепортации состоит в том, чтобы передавать из точки А в точку В не сам объект, а его квантовое состояние. Квантовая телепортация является реальностью, проверенной на практике. Она проверялась в лабораториях, правда только для очень маленьких квантовых систем. В теории возможно телепортировать сколь угодно большую квантовую систему, но пока мы не обладаем технологиями, способными выполнять телепортацию макроскопических объектов.
Нам бы хотелось телепортировать поляризоваиный фотон из точки А в точку В. Фактически, мы понимаем, что речь идет о телепортации состояния фотона. В наивном понимании телепортации нам следует измерить состояние фотона в точке А, а затем создать фотон в точке В, обладающий измеренным состоянием фотона А. Это, однако, сделать невозможно, - с помощью измерения мы не можем определить неизвестное состояние фотона, измерение безвариантно разрушает состояние.
Трюк состоит в том, чтобы телепортировать состояние не определяя, каким же является это состояние.
Как можно это сделать? Представьте себе, что у нас есть фотон в точке А в неизвестном поляризационном состоянии:

Для реализации телепортации нам следует выполнить некоторые предварительные действия. Мы должны сгенерировать запутаиную пару в состоянии  и послать первый фотон в точку А, а второй фотон в точку В.
и послать первый фотон в точку А, а второй фотон в точку В.
Теперь у нас есть три фотона, их объединенное состояние является 3кубитом, который может быть вычислен как тензорное произведение:

Далее мы собираемся смешать состояния двух фотонов в точке А, выполняя следующие ортогональные трансформации в пространстве 2-кубита:

Эта трансформация ортогональна, поскольку она трансформирует каждый базисный вектор в вектор длины 1, и скалярное произведение образов различных базисных векторов друг с другом равно нулю.
Если выполнить эту трансформацию для первых двух фотонов 3-кубита, то получим состояние:

Затем выполиим измерение первых двух фотонов в точке А. Возможны четыре различных результата: 00, 01, 10 и 11. Давайте рассмотрим все четыре случая и посмотрим, что происходит с фотоном в точке В в каждом из четырех случаев.
Случай 1. Мы наблюдаем 00 для первых двух фотонов. В этом случае 3-кубит сожмется, переходя в состояние:

которое можно рассматривать как множитель в тензорном произведении

Фактически это означает, что фотон в точке В находится в состоянии:

Случай 2. Мы наблюдаем 01 для первых двух фотонов. В этом случае фотон в точке В находится в состоянии:

Случай З. Мы наблюдаем 10 для первых двух фотонов. В этом случае фотон в точке В находится в состоянии:

Случай 4. Мы наблюдаем 11 для первых двух фотонов. В этом случае фотон в точке В находится в состоянии:

В финале выполним ортогональную трансформацию для фотона в точке В. Тин трансформации зависит от результата наблюдения в точке А.
Случай 1. Если мы наблюдали 00 для первых двух фотонов, то выполним следующую трансформацию фотона в точке В:

Случай 2. Если мы наблюдали 01 для первых двух фотонов, то выполним следующую трансформацию фотона в точке В:

Случай З. Если мы наблюдали 10 для первых двух фотонов, то выполним следующую трансформацию фотона в точке В:

Случай 4. Если мы наблюдали 11 для первых двух фотонов, то выполним следующую трансформацию фотона в точке В:
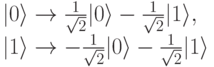
Нетрудно проверить, что во всех случаях результат трансформации будет один и тот же - фотон в точке В будет находиться в состоянии исходного фотона в точке А. Давайте для случая 1 проведем вычисления:
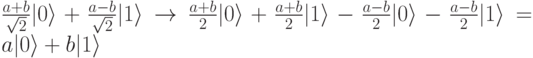
Достигнут успех - состояние в точке А телепортировано в точку В. Заметьте, ин одна из наших трансформаций не зависит от значений а и b. Трансформации, выполняемые в точке В, зависят от результатов наблюдений в А, но не от значений коэффициентов а и b, которые остаются неопределенными в течение всего процесса.
Мы показали, что телепортация состояния требует передачи материальных сущностей - двух частей запутанного кубита, которые должны быть доставлены соответственно в точки А и В. Однако это может быть сделано заранее.
Заметим также, что скорость телепортации не превышает скорости света, так что эта процедура не нарушает принципов теории относительности. В самом деле, заключительная трансформация в точке В зависит от результатов наблюдений в А. Эти результаты должны быть переданы из А в точку В, а скорость передачи этой информации ограничена скоростью света. Мы особо подчеркиваем, что передаваемая информация является классической информацией - это просто два бита, значение которых показывает, какой из четырех возможных случаев имел место. Эта информация может передаваться по обычному каналу связи.
В заключение отметим, что оригинальное квантовое состояние в точке А было разрушено. Фактически имеет место теорема, которая говорит, что неизвестное квантовое состояние нельзя дублировать, так что телепортация состояния из А в В с необходимостью требует разрушения оригинального квантового состояния в А.
