Азы (nuts and bolts) классических вычислении
Выполнение компьютерной программы сводится к последовательности выполнения команд - базисных операций, выполняемых процессором компьютера. Сегодняшние процессоры компьютера мощные и могут выполнять достаточно сложные команды. Для нашего анализа разумно вернуться к корням компьютерных вычислений и обсудить простейшие базисные операции, достаточные для построения компьютера. Таких операций три: АND, ОR, NОТ. Первые две - бинарные операции над двумя аргументами, операция NОТ - унарная, у нее один аргумент.
Логика является источником этих операций. Значения бита интерпретируются как True/Fa1se, где х = 1 интерпретируется как "х истинно" (Тrue), а х = 0 означает "х - ложно" (Fa1se). Тогда х АND у означает "х и у оба истинны", х ОR у означает "или х - истинно, или у - истинно, или х и у оба истинны". Эти операции называются булевыми операциями, названными так в честь Джорджа нуля - математика 19-го столетия, положившего начало оснований символической логики.
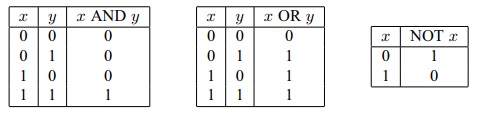
Приведем следующие истинностные таблицы этих логических операций:
Далее будем использовать более короткую нотацию "
" для " х AND у", " 
" для "х ОR у" и "
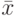" для "NОТ х". Функция АND называется также конъюнкцией, ОR - дизъюнкцией.
Утверждение. Операции Булевой логики удовлетворяют следующим свойствам - законам логики:
(1) 
,
(2) 
,
(З) 
,
(4) 
,
(5) 
.
Доказательство этих свойств оставляем в качестве упражнения.
При вычисления логических выражений важен порядок выполнения операций. Полагается, что AND выполняется раньше, чем OR, также как в арифметических выражениях умножение имеет более высокий приоритет чем сложение. Так что выражение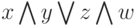 
понимается как 
, а выражение 
эквивалентно 
.
Пример. Давайте выразим функцию х = у через функции базиса. По определению эквивалентности (равенства), либо оба х и у имеют значение Тruе, либо оба - Fa1se. Это можно выразить так:
Пример. Давайте выразим функциями базиса отношение между числами: 2-битное целое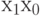 
больше чем 2-битное целое 
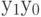. Построенная логическая функция должна давать 1, если 
и 0 в противном случае. Неравенство выполняется, если 
либо 
и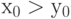 
Неравенство "" означает, что 
и 
. Выражение для равенства было приведено в предыдущем примере. Комбинируя, получим формулу булевой алгебры, вычисляющую эту функцию:
Как ранее отмечалось, любое классическое вычисление может рассматриваться как функция 
. Такая функция может быть заменена k функциями 
, где каждая функция 
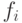определена на 
и производит вывод в 
. Функция 
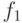вычисляет первый бит функции f, функция 
вычисляет второй бит функции f , и так далее. По этой причине сосредоточим наше внимание на вычисления функция
Мы утверждаем, что любую булеву функцию можно выразить через элементарные функции {АND, OR, NOT}. В электронике булевы функции реализуются электрическими схемами, где присутствие напряжения в проводе представляет 1, а отсутствие - О. Представьте себе, что у нас есть набор ящичков, реализующих элементарные функции {АND, OR, NОТ}. Ящичек для АND имеет два провода на входе и один на выходе. Следствием нашего утверждения является то, что, используя элементарные ящички - стандартные схемные элементы (gates - "стандартный элемент"), можно построить процессор компьютера. Фактически так и строятся компьютеры сегодня за тем исключением, что вместо использования отдельных стандартных элементов для каждой элементарной булл
Покажем теперь на примере, как можно, используя элементарные функции {АND, OR, NОТ} выразить функцию 
, заданную следующей таблицей истинности:
Рассмотрим вторую строку таблицы, которая говорит, что функция имеет значение 1, когда х = 0, у = 0, z = 1. Если построить конъюнкцию: 
, то она также будет иметь значение 1 на этом наборе переменных и будет иметь значение 0 на всех остальных наборах значений х, у, z. Рассмотрим и все другие строки таблицы, где функция f имеет значение 1. Это происходит, когда (х = 0, у = 1, z = 1) и (х = 1, у = 0, z = 0). Конъюнкции, которые генерируют 1 для этих наборов переменных, имеют вид: 
и 