Квантовое преобразование Фурье
На Шаге 2 применим трансформацию Адамара:
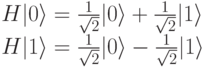
к последнему биту. В результате получим:
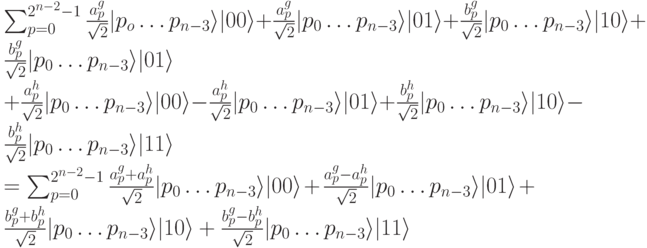
На Шаге 3 выполняется операция СNОТ на последнем бите, управляемая предпоследним битом: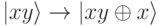 , что дает:
, что дает:
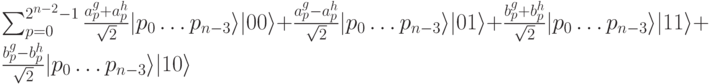
Шаг 4 более изощренный. Мы выполняем последовательность поворотов предпоследнего бита:
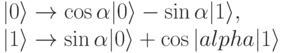
Первый поворот на угол  . Затем для каждого из первых n - 2 битов
. Затем для каждого из первых n - 2 битов 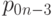 выполняем поворот предпоследнего бита на угол
выполняем поворот предпоследнего бита на угол  управляемое битом
управляемое битом 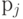 . Поворот выполняется только тогда, когда
. Поворот выполняется только тогда, когда 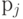 равно 1, в противном случае ничего не делается. В качестве альтернативы управляемый поворот можно интерпретировать как поворот предпоследнего бита на угол
равно 1, в противном случае ничего не делается. В качестве альтернативы управляемый поворот можно интерпретировать как поворот предпоследнего бита на угол 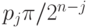 .
.
Комбинируя эти повороты вместе, получаем поворот на угол
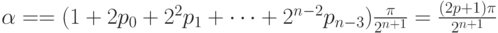
Далее в записи введем сокращение, заменяя 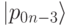 на
на 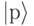 . Результатом работы Шага 4 является:
. Результатом работы Шага 4 является:
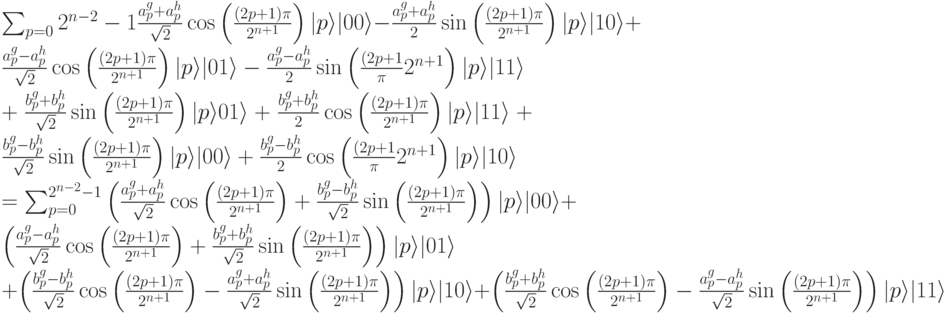
На шаге 5 применяется СNОТ к предпоследнему биту, управляемое последним битом:
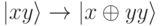
что дает:
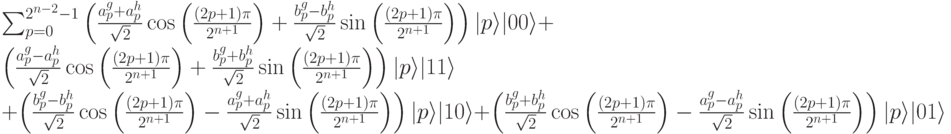
Наш завершающий шаг состоит из применения управляемого отрицания СNОТ к каждому из первых n - 2 битов, все управляемые предпоследним битом. При записи финального результата разделяем его на две части. Тогда, когда предпоследний бит равен нулю, сохраняем р как суммируемую переменную. Когда же предпоследний бит равен единице, заменяем р новой переменной r. Биты r берутся с отрицанием, результат отрицания будем обозначать как 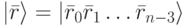 . В результате получаем следующее выражение:
. В результате получаем следующее выражение:
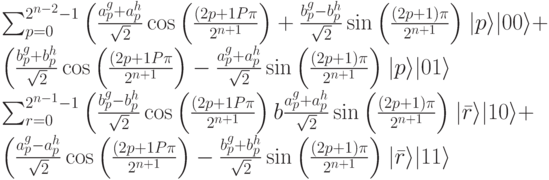
Вспоминая формулы БПФ, мы обнаруживаем, что первые два коэффициента-это и
и 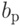 для
для 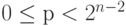 , в то время как последние два коэффициента - это
, в то время как последние два коэффициента - это  и
и 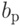 для
для 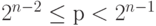 ,
, 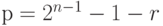 . Предыдущее выражение упрощается и имеет вид:
. Предыдущее выражение упрощается и имеет вид:
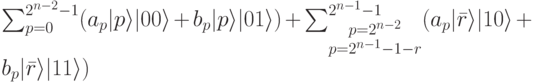
Когда 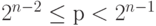 ,
, 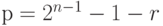 , то оно записывается как целое из n - 1 бит в бинарной форме, ведущий бит р равен 1, а остальные n - 2 бита являются отрицанием битов
, то оно записывается как целое из n - 1 бит в бинарной форме, ведущий бит р равен 1, а остальные n - 2 бита являются отрицанием битов  , так что две части суммы можно скомбинировать, рассматривая р теперь как целое из n - 1 битов,
, так что две части суммы можно скомбинировать, рассматривая р теперь как целое из n - 1 битов,
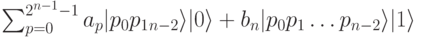
Мы видим, что в результате последовательности шагов 1-б в точности получено квантовое преобразование Фурье входа из n-кубита.
Упражнение. Покажите, что сложность квантового преобразования Фурье для п-кубита (число используемых стандартных квантовых элементов) равна 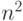 .
.
Мы видим, что КПФ имеет квадратичную сложность (как функция от числа битов), в то время как БПФ имеет экспоненциальную сложность.
