Опубликован: 24.09.2017 | Доступ: свободный | Студентов: 1239 / 371 | Длительность: 12:18:00
Тема: Менеджмент
Специальности: Менеджер, Руководитель, Экономист
Лекция 4:
Амортизация
4.3 Правило суммы лет
Правило суммы лет ПСЛ1На английском языке - Sum-of-the-Years'-Digits Depreciation. для вычисления амортизационных отчислений состоит в следующем. Если срок амортизации равен n лет, то вычисляем по формуле суммы арифметической прогрессии величину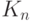 
- сумму номеров лет:
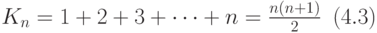
Амортизационных отчисления в i-м году вычисляется по формуле:
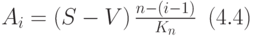
где, как и раньше, S - первоначальная стоимость имущества, V - его остаточная стоимость.
Амортизационные отчисления по ПСЛ образуют убывающую арифметическую прогрессию. Поэтому этот метод называется еще методом убывающей арифметической прогрессии. Вычислим разность этой арифметической прогрессии:
![d = A_{i+1}-A_{i}=(S-V)\,\left(\frac{n-(i+1-1)}{K_n}-\frac{n-(i-1)}{K_n}\right)=\\[4pt]
&=&\frac{S-V}{K_n}\,(-1)=-\frac{2\,(S-V)}{n(n+1)}](/sites/default/files/tex_cache/4bb04cc8b753287e70a38a73daf93c57.png)
Пример 42. Фирма из примера 41 решила ускорить процесс амортизации, применив правило суммы лет. Составим таблицу амортизационных отчислений.
Решение. Сначала вычислим сумму лет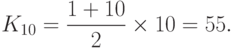 
Выпишем теперь номера лет периода амортизации в обратном порядке: 10, 9, 8, 7, 6, 5, 4, 3, 2, 1. По ПСЛ на конец первого года списывается 10/55 амортизируемой суммы (100 000 руб.), на конец второго года - 9/55 этой суммы и так далее. В конце десятого, последнего года амортизации, списывается 1/55 от амортизируемой суммы. Составим таблицу амортизационных отчислений и остаточных стоимостей по годам. Обращаем внимание читателя на то, что в этом и следующих примерах в этой лекции мы будем округлять результаты вычислений в итоговых таблицах до целых рублей.
| Год службы | Списываемая доля первоначальной стоимости | Амортизационные отчисления (руб.) | Стоимость на конец года (руб.) |
|---|---|---|---|
| 0 | 0 | 0 | 110 000 |
| 1 | 10/55 | 18 182 | 91 818 |
| 2 | 9/55 | 16 364 | 75 455 |
| 3 | 8/55 | 14 545 | 60 909 |
| 4 | 7/55 | 12 727 | 48 182 |
| 5 | 6/55 | 10 909 | 37 273 |
| 6 | 5/55 | 9 091 | 28 182 |
| 7 | 4/55 | 7 273 | 20 909 |
| 8 | 3/55 | 5 455 | 15 455 |
| 9 | 2/55 | 3 636 | 11 818 |
| 10 | 1/55 | 1 818 | 10 00 |
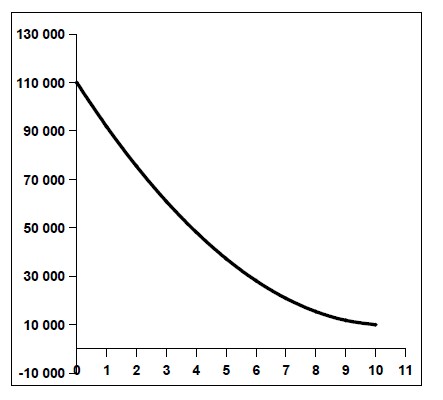
Построим график изменения балансовой стоимости прибора по годам (рис.9) при амортизации по ПСЛ. Как и в предыдущем примере, на оси абсцисс будем откладывать периоды эксплуатации (годы), а на оси ординат - значения балансовой стоимости в конце соответствующего года.
Объясним, какая математическая функция соответствует графику, приведённому на рис.9. Можно показать, что при амортизации по ПСЛ стоимость имущества в конце k~-го года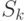 
вычисляется по формуле:
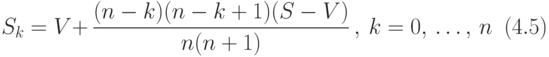
Из уравнения (4.5) следует, что график балансовой стоимости амортизируемого объекта является дугой левой ветви квадратичной параболы, которая соединяет точку с координатами (0,S) с точкой с координатами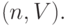 
Сравним изменение балансовой стоимости прибора по годам при РА (пример 41) и при амортизации по ПСЛ (пример 42). Результаты сравнения удобно представить в виде таблицы:
| Год службы | Стоимость на конец года (РА) (руб.) | Стоимость на конец года (ПСЛ) (руб.) | Разность (%) |
|---|---|---|---|
| 0 | 110 000 | 110 000 | 0 |
| 1 | 100 000 | 91 818 | 8.18 |
| 2 | 90 500 | 75 455 | 16.16 |
| 3 | 80 000 | 60 909 | 23.86 |
| 4 | 70 000 | 48 182 | 31.17 |
| 5 | 60 000 | 37 273 | 37.88 |
| 6 | 50 000 | 28 182 | 43.64 |
| 7 | 40 000 | 20 909 | 47.73 |
| 8 | 30 000 | 15 455 | 48.48 |
| 9 | 20 000 | 11 818 | 40.91 |
| 10 | 10 000 | 10 000 | 0.00 |
Сравнивая значения во втором и третьем столбцах последней таблицы, замечаем, что амортизация по ПСЛ действительно ускоренная: все года стоимость прибора на конец года при амортизации по ПСЛ меньше, чем при РА. Например, к концу четвертого года при РА стоимость прибора составляет 70 000 руб., а при амортизации по ПСЛ - 48 182 руб., что меньше на 31.17%.
