НОУ ИНТУИТ | Математические методы распознавания образов. Лекция 10: Селекция признаков

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 30.04.2008 | Доступ: свободный | Студентов: 1614 / 251 | Оценка: 4.24 / 3.92 | Длительность: 14:56:00

Специальности: Математик

Теги: beta, IWR, recognition, алгоритмы, базисными векторами, выпуклая оболочка, выходной нейрон, направляющий вектор, обучение, поиск, полиэдр, пространство признаков, процедуры, разработка, сложность, собственный вектор, теория, эмпирический риск

|

Вам нравится? Нравится 22 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Материалы этой лекции посвящены задаче селекции признаков. Приведены примеры практической реализации данной задачи, основные теоремы и определения

10.1. Задача селекции признаков

Рассмотрим этапы решения задачи распознавания образов:

Генерация признаков – выявление признаков, которые наиболее полно описывают объект.
Селекция признаков – выявление признаков, которые имеют наилучшие классификационные свойства для конкретной задачи.
Построение классификатора.
Оценка классификатора.

Пусть

$X\in R^m$ – множество признаков,
$Y\in R^l$ – множество признаков, которые нужно отобрать в процессе селекции, причем .

Тогда задача селекции задается следующим образом: 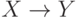$X\rightarrow Y$ .

10.1.1. Постановка задачи селекции признаков.

Пусть задан вектор признаков $X\in R^m$ . Среди них необходимо выбрать наиболее информативные, т.е. получить новый вектор признаков $Y\in R^l$ , причем l<m .

Определение. Процедура выделения из множества признаков меньшего подмножества с наилучшим сохранением информативности для классификации называется селекцией признаков.

Суть выбора признаков – это выделение признаков, которые приводят к большим расстояниям между классами и к малым внутри классов.

Зачем нужна селекция признаков?

Основной мотивацией для сокращения числа признаков является уменьшение вычислительной сложности. Наряду с признаками, имеющими низкие классификационные способности весьма вероятна ситуация двух хороших признаков (с почти равными классифицирующими способностями), сильно коррелированных между собой.

Вторая причина для уменьшения числа признаков – повышение общности классификатора.

10.1.2. Общность классификатора.

Пусть

– число прецедентов,
– число степеней свободы классификатора (для нейронной сети – это количество синаптических весов).

Ясно, что чем больше степеней свободы, тем легче настроить классификатор. Обозначим через $\frac{N}{k}$ характеристику общности. Тогда получаем, что, чем больше $\frac{N}{k}$ , чем выше общность классификатора.

Чем больше признаков, тем больше . Поэтому при ограниченном уменьшение числа признаков согласуется с уменьшением , т.е. с усложнением настройки классификатора.

Различают скалярную и векторную селекцию признаков. При скалярной селекции рассматривается отдельно один признак из данного множества. Таким образом, получили одномерную задачу. При векторной селекции одновременно исследуются свойства группы признаков.

10.2. Предобработка векторов признаков

Пусть задано множество признаков.

Селекции признаков предшествует предобработка, позволяющая привести их в единый масштаб измерений и произвести некоторые дополнительные улучшения.

Основные операции предобработки описываются следующими тремя пунктами.

10.2.1. Удаление выбросов – точек, лежащих "очень далеко" от среднего значения. Обычно измеряется расстояние в средних отклонениях, например, $2\sigma\sim 95\%$ , $3\sigma\sim 99\%$ для нормального распределения.

10.2.2. Нормализация. Признаки, имеющие большие значения, могут влиять на классификатор сильнее остальных, что искажает правильность классификатора. Поэтому необходимо уменьшить их влияние путем, который носит название нормализации. Пусть

– прецедент,
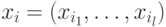$x_i=(x_{i_1},\ldots,x_{i_l})$ – признаки.

Тогда

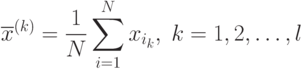
$\overline{x}^{(k)}=\frac{1}{N}\sum_{i=1}^N x_{i_k},\;k=1,2,\ldots,l$

есть усреднение признака (фактически его математическое ожидание).

Обозначим через

$(\sigma^{(k)})^2=\frac{1}{N-1}\sum_{i=1}^N(x_{i_k}-\overline{x}^{(k)})^2$

оценку разброса. Тогда нормализованные признаки задаются следующим образом

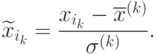
$\widetilde{x}_{i_k}=\frac{x_{i_k}-\overline{x}^{(k)}}{\sigma^{(k)}}.$

10.2.3. Пропуск данных (потери). По многим прецедентам могут быть известны не все признаки. В таком случае, если данных много, то можно отобрать те у которых набор признаков одинаковый. Если же отбрасывать признаки нельзя, то их можно дополнить, например, с помощью эвристик.

Дальше >>

Авторизоваться

Математические методы распознавания образов

Селекция признаков

10.1. Задача селекции признаков

10.2. Предобработка векторов признаков

Вопросы и ответы