Линейный классификатор. Алгоритм персептрона
3.1. Линейная дискриминантная функция
Рассмотрим задачу построения линейной разделяющей гиперповерхности. Главным достоинством линейного классификатора является его простота и вычислительная эффективность.
Рассмотрим линейную дискриминантную функцию:  ,
где
,
где 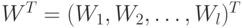 – весовой вектор,
– весовой вектор, 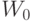 – порог. Поведение решения задается уравнением
– порог. Поведение решения задается уравнением  . Пусть
. Пусть  и
и  – два конечных множества векторов признаков в евклидовом пространстве,
относящихся к классу
– два конечных множества векторов признаков в евклидовом пространстве,
относящихся к классу 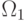 и
и 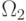 соответственно,
т.е
соответственно,
т.е  принадлежит классу
принадлежит классу 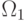 при
при  , а
, а  принадлежит классу
принадлежит классу 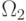 при
при  .
.
Задача состоит в том, чтобы:
- установить разделимость этих множеств;
- найти разделяющую гиперплоскость.
Рассмотрим сначала в качестве примера двумерную задачу, когда образы представляются точками на плоскости.
Определение. Множество, содержащее отрезок, соединяющий две произвольные внутренние точки, называется выпуклым.
Определение. Выпуклая оболочка – это минимальное выпуклое множество, содержащее данное.
Утверждение 3.1. Два множества на плоскости линейно разделимы тогда и только тогда, когда их выпуклые оболочки не пересекаются.
Из этого утверждения получаем следующее правило проверки разделимости множеств на плоскости:
- Построить выпуклые оболочки.
- Проверить пересечение выпуклых оболочек. Если они не пересекаются, то множества разделимы.
Очевидно и правило, по которому можно найти разделяющую прямую:
- Найти ближайшую пару точек в выпуклых оболочках обоих множеств.
- Построить срединный перпендикуляр к отрезку, соединяющему эти точки. Этот перпендикуляр и будет разделяющей прямой.
Пусть размерность вектора признаков  и вектора коэффициентов
и вектора коэффициентов  равна
равна  . Рассмотрим "пополненные" вектора
. Рассмотрим "пополненные" вектора  следующего вида:
следующего вида:  – пополненный весовой вектор,
– пополненный весовой вектор, 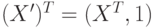 – пополненный вектор признаков.
Рассмотрим также в
– пополненный вектор признаков.
Рассмотрим также в  -мерном пространстве однородную линейную функцию
-мерном пространстве однородную линейную функцию 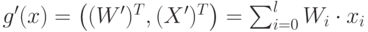 .
.
Очевидно следующее
Утверждение 3.2. Множества  и
и  линейно разделимы в пространстве
линейно разделимы в пространстве 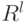 дискриминантной функцией
дискриминантной функцией  тогда и только тогда, когда они
разделимы в пополненном пространстве
тогда и только тогда, когда они
разделимы в пополненном пространстве  однородной дискриминантной
функцией
однородной дискриминантной
функцией 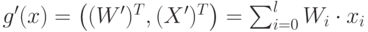 .
.
Далее будем рассматривать дискриминантные функции и вектора в пополненном пространстве.
Определение. Множество  называется симметричным множеством к множеству
называется симметричным множеством к множеству  .
.
Утверждение 3.3. Два замкнутых множества  и
и  разделимы тогда и только тогда, когда выпуклая оболочка множества
разделимы тогда и только тогда, когда выпуклая оболочка множества  не содержит начала координат.
не содержит начала координат.
Доказательство. Пусть множества  и
и  разделимы. Тогда существует
линейная функция
разделимы. Тогда существует
линейная функция  такая, что
такая, что  при
при  и
и  при
при  . Рассмотрим множество
. Рассмотрим множество  ,
тогда
,
тогда  при
при  . Следовательно,
. Следовательно,  для выпуклой линейной комбинации из
для выпуклой линейной комбинации из  , а это означает, что
, а это означает, что  , т.к.
, т.к.  – замкнутое. Здесь
– замкнутое. Здесь  обозначает начало
координат.
обозначает начало
координат.
Пусть  , и пусть
, и пусть 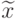 – ближайшая к началу координат
– ближайшая к началу координат  точка из
точка из 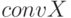 .
Плоскость
.
Плоскость  с направляющим вектором
с направляющим вектором  не пересекает
не пересекает 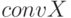 ,
а, значит,
,
а, значит,  на
на  . Следовательно,
. Следовательно,  на
на  .
.

