НОУ ИНТУИТ | Математические методы распознавания образов. Лекция 4: Оптимальная разделяющая гиперплоскость

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 30.04.2008 | Доступ: свободный | Студентов: 1617 / 252 | Оценка: 4.24 / 3.92 | Длительность: 14:56:00

Специальности: Математик

Теги: beta, IWR, recognition, алгоритмы, базисными векторами, выпуклая оболочка, выходной нейрон, направляющий вектор, обучение, поиск, полиэдр, пространство признаков, процедуры, разработка, сложность, собственный вектор, теория, эмпирический риск

|

Вам нравится? Нравится 22 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Материалами данной лекции рассматривается вопрос существования и единственности оптимальной разделяющей гиперплоскости. Приведены примеры её построения, а также основные теоремы и определения

Ключевые слова: конечные, множества, гиперплоскость, функция, максимум, значение, неравенство, выпуклая оболочка, минимум

4.1. Существование и единственность

Пусть и $\overline{X}$ - конечные множества точек в евклидовом пространстве R^l .

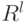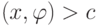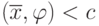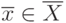Определение. и $\overline{X}$ разделимы гиперплоскостью, если существует единичный вектор $\varphi$ и число , что $(x,\varphi)>c$ при $x\in X$ , $(\overline{x},\varphi)<c$ при $\overline{x}\in\overline{X}$ .

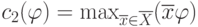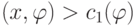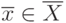Обозначим $c_1(\varphi)=\min_{x\in X}(x,\varphi)$ , $c_2(\varphi)=\max_{\overline{x}\in\overline{X}}(\overline{x}\varphi)$ . Тогда $(x,\varphi)>c_1(\varphi)$ при $x\in X$ , $(\overline{x},\varphi)<c_2(\varphi)$ при $\overline{x}\in\overline{X}$ . Если $c_1(\varphi)\geq c_2(\varphi)$ , то гиперплоскость

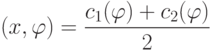$(x,\varphi)=\frac{c_1(\varphi)+c_2(\varphi)}{2}$

( 4.1)

разделяет

и $\overline{X}$ .

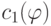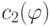В силу непрерывности $c_1(\varphi)$ и $c_2(\varphi)$ существует множество разделяющих гиперплоскостей, если существует (4.1).

Определение. Оптимальной называется разделяющая гиперплоскость (4.1), соответствующая вектору 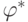$\varphi^*$ , при котором достигается максимум $\Pi(\varphi)$ .

Теорема. Если два множества и $\overline{X}$ разделимы гиперплоскостью, то оптимальная разделяющая гиперплоскость существует и единственна.

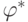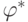Доказательство. Функция $\Pi(\varphi)$ непрерывна на сфере $|\varphi|\leq 1$ . Значит, $\max_{|\varphi|\leq 1}\Pi(\varphi)$ существует и достигается при некотором значении $\varphi^*$ . Предположим, что он достигается внутри сферы, т.е. $|\varphi^*|<1$ . Тогда для $\varphi^{**}=\frac{\varphi^*}{|\varphi^*|}$ получаем

$\begin{gathered} \Pi(\varphi^{**})=c_1(\varphi^{**})-c_2(\varphi^{**})= \\ = \min_{x\in X}(x,\varphi^{**})-\max{\overline{x}\in\overline{X}}(\overline{x},\varphi^{**})= \\ = \frac{1}{|\varphi^*|}\Pi(\varphi^*)>\Pi(\varphi^*), \end{gathered}$

что противоречит предположению о том, что $\varphi^*$ - точка максимума $\Pi(\varphi)$ .

Следовательно, максимум достигается на границе сферы, т.е. $|\varphi^*|=1$ .

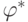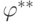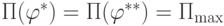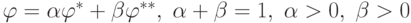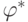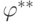Докажем единственность максимума. Предположим, что это не так и существуют различные $\varphi^*$ и $\varphi^{**}$ такие, что $\Pi(\varphi^*)=\Pi(\varphi^{**})=\Pi_{\max}$ . Рассмотрим значение $\varphi=\alpha\varphi^*+\beta\varphi^{**},\; \alpha+\beta=1, \; \alpha>0,\;\beta>0$ , не совпадающее ни с $\varphi^*$ , ни с $\varphi^{**}$ .

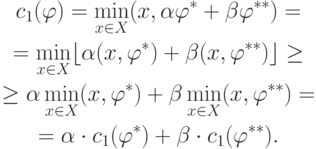
$\begin{gathered} c_1(\varphi)=\min_{x\in X}(x,\alpha\varphi^*+\beta\varphi^{**})= \\ =\min_{x\in X}\lfloor\alpha(x,\varphi^*)+\beta(x,\varphi^{**})\rfloor\geq \\ \geq\alpha\min_{x\in X}(x,\varphi^*)+\beta\min_{x\in X}(x,\varphi^{**})= \\ =\alpha\cdot c_1(\varphi^*)+\beta\cdot c_1(\varphi^{**}). \end{gathered}$

Аналогично $c_2(\varphi)\leq\alpha\cdot c_2(\varphi^*)+\beta\cdot c_2(\varphi^{**})$ .

Тогда

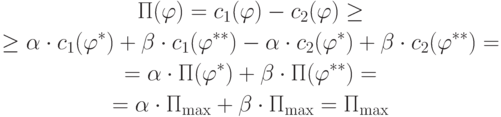
$\begin{gathered} \Pi(\varphi)=c_1(\varphi)-c_2(\varphi)\geq \\ \geq\alpha\cdot c_1(\varphi^*)+\beta\cdot c_1(\varphi^{**})-\alpha\cdot c_2(\varphi^*)+\beta\cdot c_2(\varphi^{**})=\\ =\alpha\cdot\Pi(\varphi^*)+\beta\cdot\Pi(\varphi^{**})= \\ =\alpha\cdot\Pi_{\max}+\beta\cdot\Pi_{\max}=\Pi_{\max} \end{gathered}$

и $\varphi$ - тоже значение, на котором достигается максимум.

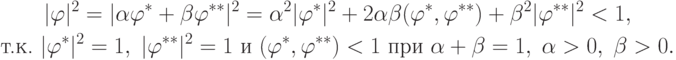
$\begin{gathered} |\varphi|^2=|\alpha\varphi^*+\beta\varphi^{**}|^2=\alpha^2|\varphi^*|^2+2\alpha\beta(\varphi^*,\varphi^{**})+\beta^2|\varphi^{**}|^2<1,\\ \text{т.к. }|\varphi^*|^2=1,\; |\varphi^{**}|^2=1 \text{ и } (\varphi^*,\varphi^{**})<1\text{ при }\alpha+\beta=1,\;\alpha>0,\;\beta>0. \end{gathered}$

Но $\varphi$ лежит внутри сферы $|\varphi|\leq1$ и поэтому не может быть точкой максимума. Следовательно, предположение о существовании двух максимумов неверно и максимум единственный.

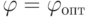Таким образом, если максимум функции $\Pi(\varphi)$ достигается при значении $\varphi=\varphi_{опт}$ , то гиперплоскость $(x,\varphi_{опт})=\frac{c_1(\varphi_{опт})+c_2(\varphi_{опт})}{2}$ максимально удалена от и $\overline{X}$ и разделяет их.

Дальше >>

Авторизоваться

Математические методы распознавания образов

Оптимальная разделяющая гиперплоскость

4.1. Существование и единственность

Вопросы и ответы