Метод потенциальных функций
Рассмотрим множество прецедентов. Пусть каждый из них имеет поле притяжения. Берем новый объект и смотрим, каким классом притягивается.
Пусть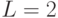 
– число классов. Обозначим эти классы через 
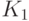и 
соответственно. Рассмотрим обучающую последовательность 
.
Без ограничения общности будем считать, что 
и 
.
Каждая точка образует в пространстве признаков 
некоторое поле
притяжения. Например, можно рассматривать каждую точку как единичный
заряд. Поле описывается потенциалом, создаваемым системой зарядов во
всем пространстве.
В пространстве задана потенциальная метрика: 
–
потенциальная функция, 
такая, что
– монотонно убывающая функция и 
– ее максимальное значение.Пример. Пусть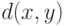 
– расстояние в 
.
Рассмотрим функцию 
. Пусть 
–
параметр функции. Рассмотрим два примера функций 
:
Пусть и 
– прецеденты первого и второго класса соответственно, 
– пробный образ. Тогда потенциалы, создаваемые в пространстве точками
из классов и будут иметь вид:
Тогда правило классификации можно записать следующим образом:
Если 
то пробный образ относится к классу , иначе к классу , при
равенстве выдавать ответ "не знаю" (отказ от распознавания).
Если рассмотреть дискриминантную функцию 
, то задача сводится к
поиску этой функции по обучающей последовательности.
Рассмотрим вариант метода потенциальных функций называется
"наивным". Он имеет следующие недостатки. Если, например, в
первом классе точек много больше, чем в остальных, то голоса первого
класса подавят голоса других классов, то есть потенциал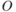 
больше
потенциала 
(рис. слева). Но даже, если множества соизмеримы, могут
возникнуть проблемы другого характера, например, погружение одних
точек в другие (рис. справа). Поэтому наивный метод подлежит
усовершенствованию.
