НОУ ИНТУИТ | Математические методы распознавания образов. Лекция 11: Методы генерации признаков

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 30.04.2008 | Доступ: свободный | Студентов: 1616 / 252 | Оценка: 4.24 / 3.92 | Длительность: 14:56:00

Специальности: Математик

Теги: beta, IWR, recognition, алгоритмы, базисными векторами, выпуклая оболочка, выходной нейрон, направляющий вектор, обучение, поиск, полиэдр, пространство признаков, процедуры, разработка, сложность, собственный вектор, теория, эмпирический риск

|

Вам нравится? Нравится 22 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются методы генерации признаков. Приведены практические примеры, основные определения и теоремы

11.1. Генерация признаков на основе линейных преобразований

В данном разделе рассматриваются способы генерации признаков через линейные преобразования исходных измерений образов. Целью такой генерации признаков является сокращение информации до "значимой", т.е. надо просто преобразовать исходное множество измерений в новое множество признаков. Обычно задача состоит в выделении низкочастотных компонент, содержащих основную информацию.

11.1.1. Базисные вектора

Пусть

$x(0),x(1),\ldots,x(N-1)$ – множество исходных измерений,
$X^T=[x(0),\ldots,x(N-1)]$ – соответствующий вектор столбец.

Рассмотрим унитарную матрицу $A_{N\times N}$ . Для действительной матрицы $A_{N\times N}$ условие унитарности обозначает, что матрица $A_{N\times N}$ ортогональная, т.е. $A_{N\times N}^{-1}=A_{N\times N}^T$ . Для комплексной матрицы $A_{N\times N}$ условие унитарности обозначает, что $A_{N\times N}^{-1}=A_{N\times N}^H$ , где матрица $A_{N\times N}^H$ - транспонированная (сопряженная).

Пусть

$y=A^H X= \left( \begin{gathered} a_0^H \\ a_1^H \\ \vdots \\ a_{N-1}^H \end{gathered} \right) \cdot X$

где $a_0^H,a_1^H,\ldots,a_{N-1}^H$ – строки из транспонированных столбцов a_i

и $A=(a_0,a_1,\ldots,a_{N-1})$ . Тогда

$x=(AA^{-1})x=(AA^H)x=AA^H x=Ay=\sum_{i=0}^{N-1}y(i)a_i.$

Вектора a_i называются базисными векторами. Таким образом, в силу ортогональности a_i между собой, y(i) – это проекция вектора на базисные вектора.

11.1.2. Случай двумерных образов.

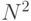Пусть $x(i,j),\;i,j=0,1,\ldots,N-1$ – двумерные измерения. Очевидно, что представление его в виде вектора размерности N^2 неэффективно. Альтернативой является преобразование через базисные матрицы.

Пусть 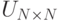$U_{N\times N}$ и $V_{N\times N}$ – унитарные матрицы. Определим матрицу преобразования в :

Учитывая, что $\def\I{\mathop{I}} UU^H=\I\limits^{.}$ и $\def\I{\mathop{I}} VV^H=\I\limits^{.}$ , имеем

Следовательно

$X=\sum_{i=0}^{N-1}\sum_{J=0}^{N-1}Y(i,j)\cdot u_i\cdot\nu_j^H$

( 11.1)

Пусть

$U=(u_0,u_1,\ldots,u_{N-1})$ , где – вектор-столбец,
$V=(\nu_0,\nu_1,\ldots,\nu_{N-1})$ , где $\nu_j^H$ – вектор-строка.

Тогда

$A_{ij}=u_i\nu_j^H= \begin{pmatrix} u_{i,0}\nu_{j,0}^* & u_{i,0}\nu_{j,1}^* & \ldots & u_{i,0}\nu_{j,N-1}^* \\ u_{i,1}\nu_{j,0}^* & u_{i,1}\nu_{j,1}^* & \ldots & u_{i,1}\nu_{j,N-1}^* \\ \vdots & \vdots & \ddots & \vdots \\ u_{i,N-1}\nu_{j,0}^* & u_{i,N-1}\nu_{j,1}^* & \ldots & u_{i,N-1}\nu_{j,N-1}^* \end{pmatrix}.$

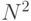Таким образом (11.1) есть выражение в терминах N^2 базисных матриц. Если – диагональная, то (X=\sum_{i=0}^N-1) – это разложение по базисным матрицам или образам.

Также возможна следующая запись:

$Y(i,j)=X,\langle A_{ij}\rangle.$

Тогда

$\langle A,B\rangle=\sum_{m=0}^{N-1}\sum_{n=0}^{N-1}A(m,n)\cdot B^*(m,n).$

Дальше >>

Авторизоваться

Математические методы распознавания образов

Методы генерации признаков

11.1. Генерация признаков на основе линейных преобразований

Вопросы и ответы