Контекстно-зависимая классификация
9.1. Постановка задачи
Рассмотренные ранее задачи предполагали, что нет зависимости между
различными классами, т.е. имея вектор  из класса
из класса 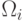 , мы могли получить
следующий вектор из любого класса. Далее мы будем предполагать
зависимость классов, т.е. классификация каждого нового вектора
осуществляется в зависимости от классификации предыдущих векторов.
Выбор класса, к которому следует отнести вектор, зависит от его
собственного значения, значений других векторов, существующих
отношений между различными классами.
, мы могли получить
следующий вектор из любого класса. Далее мы будем предполагать
зависимость классов, т.е. классификация каждого нового вектора
осуществляется в зависимости от классификации предыдущих векторов.
Выбор класса, к которому следует отнести вектор, зависит от его
собственного значения, значений других векторов, существующих
отношений между различными классами.
Такие задачи возникают во многих приложениях: распознавание речи, обработка изображений и др.
Эта классификация называется контекстно-зависимой.
Отправной точкой является Байесовский классификатор. Но зависимость
между различными классами требует более общей формулировки проблемы.
Общая информация, которая присутствует в векторах, требует, чтобы
классификация была выполнена с использованием всех векторов
одновременно и также была организованна в той же последовательности, в
которой получена в экспериментах. Поэтому мы будем называть вектор
признаков наблюдением, выстроенным в последовательность 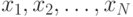 из
из  наблюдений.
наблюдений.
9.2. Байесовский классификатор
Пусть 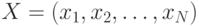 – последовательность
– последовательность  наблюдений и
наблюдений и  – классы, в
которые эти вектора можно классифицировать. Пусть также
– классы, в
которые эти вектора можно классифицировать. Пусть также 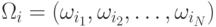 – одна из
возможных последовательностей соответствия классов последовательности
наблюдений, где
– одна из
возможных последовательностей соответствия классов последовательности
наблюдений, где  ,
,  .
Общее число таких последовательностей классов
.
Общее число таких последовательностей классов 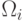 есть
есть 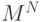 .
Задача заключается в том, чтобы решить, к какой последовательности классов отнести
последовательность наблюдений. Это эквивалентно отнесению
.
Задача заключается в том, чтобы решить, к какой последовательности классов отнести
последовательность наблюдений. Это эквивалентно отнесению  к
к 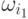 ,
,  к
к 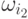 и т.д.
и т.д.
Подходом к решению проблемы является рассмотрение каждой конкретной
последовательности  как расширенного вектора признаков на
как расширенного вектора признаков на 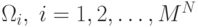 как на возможных классах.
В данном случае Байесовское правило
как на возможных классах.
В данном случае Байесовское правило


9.3. Модель Марковской цепи
Одна из наиболее используемых моделей, описывающих зависимость
классов, является правило Марковской цепи. Если 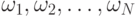 есть
последовательность классов, то Марковская модель предполагает, что
есть
последовательность классов, то Марковская модель предполагает, что

Тогда зависимость классов ограничивается только внутри двух последовательных классов. Такой класс моделей называется Марковской моделью первого порядка. Возможны обобщения на второй, третий и т.д. порядок.
Другими словами, даны наблюдения 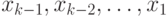 ,
принадлежащие классам
,
принадлежащие классам  соответственно. Вероятность того, что наблюдение
соответственно. Вероятность того, что наблюдение  на шаге
на шаге  принадлежит классу
принадлежит классу 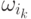 , зависит только от того класса, к которому
принадлежит наблюдение
, зависит только от того класса, к которому
принадлежит наблюдение 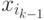 на шаге
на шаге  .
.
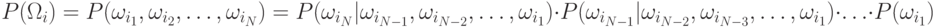
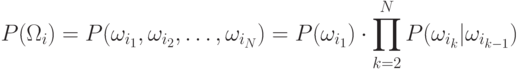 |
( 9.1) |
Сделаем два общих предположения:
- в последовательности классов наблюдения статистически независимы;
- функция плотности вероятностей в одном классе не зависит от других классов.
Это означает, что зависимость существует только на последовательности, в которой классы встречаются, но внутри классов наблюдений "подчиняются" собственным правилам. Таким образом, получаем, что
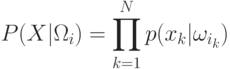 |
( 9.2) |
Комбинируя (9.1) и (9.2), получаем Байесовское правило в виде следующего утверждения.
Байесовское правило: для последовательности наблюдений
векторов 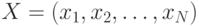 проводим их классификацию в соответствующие
последовательности классов
проводим их классификацию в соответствующие
последовательности классов 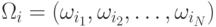 так, чтобы величина
так, чтобы величина
 |
( 9.3) |
Поиск требует вычисления последнего выражения для каждого 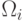 ,
, 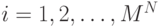 , что, в свою очередь, требует
, что, в свою очередь, требует 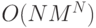 умножений,
а это очень много. Но существуют пути экономии вычислений. Если в
умножений,
а это очень много. Но существуют пути экономии вычислений. Если в 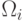 и
и 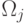 отличаются только последние классы, т.е.
отличаются только последние классы, т.е.  ,
при
,
при  и
и 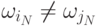 , то большая часть вычислений
дублируется.
, то большая часть вычислений
дублируется.
