Селекция признаков
10.5. Оптимальная селекция признаков
Существуют две формы использования критериев (мер отделимости классов): "пассивная" и "активная". Пассивная селекция – это работа с уже полученными признаками. Активная селекция аналогична процессу генерации признаков: она позволяет построить из исходного набора признаков новый набор меньшего размера, в котором состав признаков, вообще говоря, не является подмножеством исходного набора признаков. Все типы селекции, рассмотренные в предыдущих разделах – пассивные.
Пусть  и
и 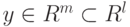 .
Рассмотрим конструирование критериев с использованием активной селекции:
.
Рассмотрим конструирование критериев с использованием активной селекции: 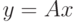 или y=F(x).
или y=F(x).
Пусть
-
 и
и  – вектора столбцы, тогда
– вектора столбцы, тогда 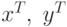 – строки,
– строки, -
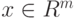 – исходное пространство признаков,
– исходное пространство признаков, -
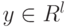 – результирующее пространство признаков,
– результирующее пространство признаков, -
 – матрица преобразования исходного пространства в результирующее,
– матрица преобразования исходного пространства в результирующее, -
 – число классов.
– число классов.
Тогда
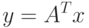
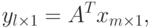
 имеет размер
имеет размер 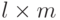 .
.Рассмотрим критерий  .
Будем максимизировать критерий
.
Будем максимизировать критерий 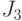 путем
выбора матрицы
путем
выбора матрицы  . Для вектора признаков
. Для вектора признаков  имеем матрицы
имеем матрицы  и
и  . Для
вектора признаков
. Для
вектора признаков  имеем матрицы
имеем матрицы 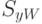 и
и 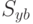 .
.
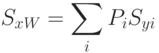
Проведем несколько преобразований.
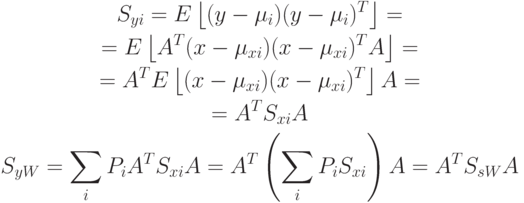
Аналогично:  . Тогда
. Тогда 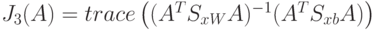 – критерий разделимости вектора признаков.
– критерий разделимости вектора признаков.
Теперь необходимо преобразовать  из соображений
из соображений 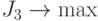 .
Будем искать решение из условия максисума
.
Будем искать решение из условия максисума
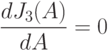
Утверждение о вычислении производной. Пусть  и
и 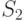 - некоторые квадратные матрицы размера
- некоторые квадратные матрицы размера 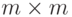 . Тогда
. Тогда
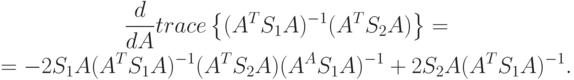
Для получения максимума по критерию, необходимо, чтобы
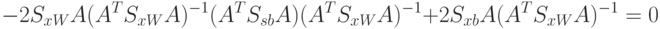
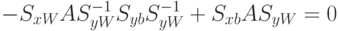

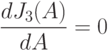
Утверждение. Пусть 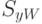 и
и 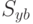 – симметрические, положительно
определенные матрицы. Тогда существует преобразование, приводящее одну
из них к единичной, а другую к диагональной.
– симметрические, положительно
определенные матрицы. Тогда существует преобразование, приводящее одну
из них к единичной, а другую к диагональной.
Доказательство. Приведем эти преобразования
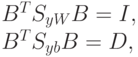
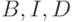 – матрицы размера
– матрицы размера  .
.Утверждение. 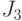 инвариантно
относительно преобразований вектора
инвариантно
относительно преобразований вектора  в
в 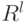 .
.
Доказательство. Рассмотрим
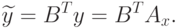

Т.к. 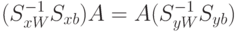 – условие того,
что производная равна нулю, то
– условие того,
что производная равна нулю, то
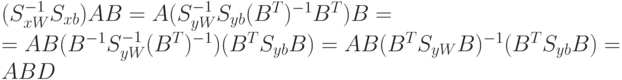
Используя предыдущее утверждение, подбираем матрицу  и получаем:
и получаем:
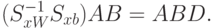
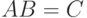 – матрица размера
– матрица размера 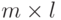 .
.Утверждение. Если матрица  положительно определенная (положительно полуопределенная), то
положительно определенная (положительно полуопределенная), то
-
все собственные значения
 положительны,
положительны, -
если
 симметричная, то все собственные вектора,
соответствующие разным собственным значениям, ортогональны,
симметричная, то все собственные вектора,
соответствующие разным собственным значениям, ортогональны, -
для симметричной матрицы
 существует преобразование
существует преобразование 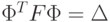 , где
, где  состоит из собственных векторов этой матрицы или столбцы
состоит из собственных векторов этой матрицы или столбцы ![\Phi=[\nu_1,\nu_2,\ldots,\nu_m]](/sites/default/files/tex_cache/73694891736a2c3648a3402e6a3aed33.png) – собственные вектора, причем
– собственные вектора, причем  – диагональная
матрица, на диагоналях которой стоят собственные значения.
– диагональная
матрица, на диагоналях которой стоят собственные значения.
Т.к. случайные величины ортогональны, то  .
.
Теперь рассмотрим алгоритм оптимальной селекции признаков:
Поиск собственных значений и выбор  наилучших (наибольших).
наилучших (наибольших).
Формирование матрицы  из собственных векторов, соответствующих этим собственным значениям
из собственных векторов, соответствующих этим собственным значениям
10.6. Оптимальная селекция признаков с помощь нейронной сети
Пусть задано  признаков,
признаков,  – вектор
признаков. Для применения теории нейронных сетей к задаче селекции
признаков немного изменим обычное представление о нейронной сети.
Теперь будем рассматривать нейронную сеть с линейными функциями
активации. Таким образом, теперь вектор признаков, попавший на вход
нейронной сети, просто суммируется и подается на выход, т.е. выход
нейрона превращается в обычную сумму.
– вектор
признаков. Для применения теории нейронных сетей к задаче селекции
признаков немного изменим обычное представление о нейронной сети.
Теперь будем рассматривать нейронную сеть с линейными функциями
активации. Таким образом, теперь вектор признаков, попавший на вход
нейронной сети, просто суммируется и подается на выход, т.е. выход
нейрона превращается в обычную сумму.
Рассмотрим так называемую автоассоциативную сеть. Сеть имеет  входных и
входных и  выходных узлов и единственный
скрытый слой с
выходных узлов и единственный
скрытый слой с  узлами и линейными функциями активации.
В процессе обучения выходы сети те же, что и входы. Такая сеть имеет
единственный максимум и выходы скрытого слоя определяют проекцию
узлами и линейными функциями активации.
В процессе обучения выходы сети те же, что и входы. Такая сеть имеет
единственный максимум и выходы скрытого слоя определяют проекцию  -мерного пространства на
-мерного пространства на  -мерное
подпространство.
-мерное
подпространство.
Интерес представляет выходной слой из  нейронов. Если
восстанавливать исходный вектор с целью максимального правдоподобия,
то получим задачу квадратичного программирования с одним
экстремумом.
нейронов. Если
восстанавливать исходный вектор с целью максимального правдоподобия,
то получим задачу квадратичного программирования с одним
экстремумом.

 .
. .
.