Комитетные методы решения задач распознавания
7.4. Функция Шеннона
Пусть 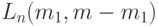 – это число гиперплоскостей, достаточное для разделения
любых точечных множеств
– это число гиперплоскостей, достаточное для разделения
любых точечных множеств  и
и  точек общего положения в пространстве
точек общего положения в пространстве 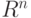 .
.
Лемма 1. Если  , то
, то

Доказательство. Если  , то добавим точки общего положения до
, то добавим точки общего положения до  .
Через
.
Через  точек из
точек из  проводим гиперплоскость:
проводим гиперплоскость:

Для  такого, что
такого, что  .
.
Выберем  и возьмем
гиперплоскости
и возьмем
гиперплоскости  и
и  .
. 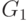 и
и 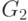 отделяют точки
отделяют точки  от
всех остальных.
от
всех остальных.
Аналогичным образом из оставшихся  точек выделяем еще
точек выделяем еще  и строим
еще пару гиперплоскостей. Далее из оставшихся
и строим
еще пару гиперплоскостей. Далее из оставшихся  точек выделяем еще
точек выделяем еще  и
строим еще пару гиперплоскостей и т.д. В конце получим
и
строим еще пару гиперплоскостей и т.д. В конце получим  точек.
Следовательно:
точек.
Следовательно:
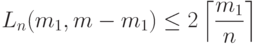
Утверждение 1. Если 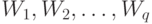 разделяют
множества
разделяют
множества  и
и  , и
, и 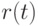 – непрерывная кривая в
– непрерывная кривая в 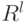 такая, что
такая, что  , а
, а  , то существует
, то существует 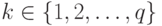 и
и  такие, что
такие, что 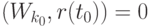 .
.
Утверждение 2. Любая гиперплоскость пересекает кривую 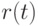 не более, чем в
не более, чем в  точках.
точках.
Доказательство. Рассмотрим линейный функционал  . Запишем условие
пересечения гиперплоскости и кривой
. Запишем условие
пересечения гиперплоскости и кривой 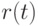 :
:
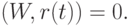
Кривая 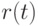 задана многочленом степени
задана многочленом степени  .
Следовательно,
.
Следовательно,  – то же многочлен степени
– то же многочлен степени  .
Значит, уравнение
.
Значит, уравнение 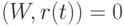 является уравнением степени
является уравнением степени  .
Следовательно, т.к. корни могут быть кратными, данное уравнение
имеет не более
.
Следовательно, т.к. корни могут быть кратными, данное уравнение
имеет не более  корней.
корней.
Лемма 2.  .
.
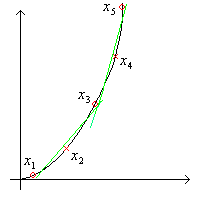
Доказательство. Построим 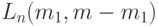 . Рассмотрим последовательность точек:
. Рассмотрим последовательность точек:

Пусть  , где
, где  ,
,  .
Тогда
.
Тогда 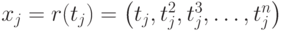 – точки в
– точки в 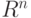 .
.
Без ограничения общности положим 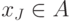 , при
, при  нечетном,
и
нечетном,
и  , при
, при  четном. Тогда получим непрерывную кривую (см. рис).
четном. Тогда получим непрерывную кривую (см. рис).
Каждая гиперплоскость дает не более, чем  пересечений. Кривая
должна иметь
пересечений. Кривая
должна иметь  разделение, т.е. должно быть
разделение, т.е. должно быть  гиперплоскостей.
Следовательно, всего гиперплоскостей должно быть не менее, чем
гиперплоскостей.
Следовательно, всего гиперплоскостей должно быть не менее, чем  ,
т.е.
,
т.е.  .
.
Т.к.


Следовательно, 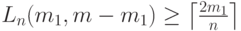 , при нечетном
, при нечетном  ,
,  , при четном
, при четном  .
.
Окончательно получаем:  ,
, 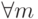 .
.
Пример. Пусть  ,
,  ,
, 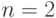 .
Обозначим
.
Обозначим 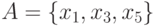 и
и  . Тогда
. Тогда

7.5. Метод построения комитета.
Пусть  – множество прецедентов;
– множество прецедентов;  в – размерность пространства
признаков;
в – размерность пространства
признаков;  и
и  – количество прецедентов в каждом классе.
– количество прецедентов в каждом классе.
Построим  – линейный функционал такой, что, если
– линейный функционал такой, что, если 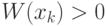 , то объект из
класса
, то объект из
класса  , и, если
, и, если 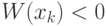 , то объект из класса
, то объект из класса 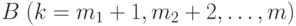 . Если данный
функционал правильно классифицирует меньше половины объектов, то
возьмем его со знаком минус.
. Если данный
функционал правильно классифицирует меньше половины объектов, то
возьмем его со знаком минус.
Итак, пусть линейный функционал  правильно классифицирует больше
половины объектов. Разобьем множество прецедентов
правильно классифицирует больше
половины объектов. Разобьем множество прецедентов  на множество
правильно классифицированных объектов
на множество
правильно классифицированных объектов  и множество неправильно
классифицированных объектов
и множество неправильно
классифицированных объектов  , т.е.
, т.е. 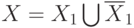 .
.
Далее строим последовательно пары функционалов 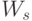 и
и  :
:
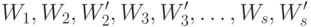
Делаем очередной шаг. 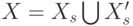 . Пусть на
. Пусть на  –
–  правильно
классифицированных объектов, а на
правильно
классифицированных объектов, а на  –
–  правильно классифицированных
объектов. Строим пару
правильно классифицированных
объектов. Строим пару 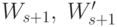 . В
. В  выделяем
выделяем  точек одного класса. Эти точки можно перевести в
точек одного класса. Эти точки можно перевести в  , т.е.
, т.е. 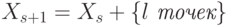 , а
, а 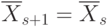 .
.
На каждом шаге множество неправильно классифицированных объектов
уменьшается на  , следовательно, процесс сходится.
, следовательно, процесс сходится.
Общее число функционалов: 
Теорема. Существует комитет
линейных функционалов, в котором число членов не превосходит  .
.