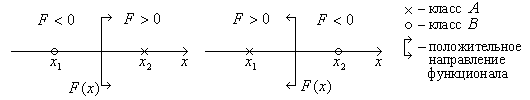Комитетные методы решения задач распознавания
7.3. Комитеты линейных функционалов
Пусть  ,
, 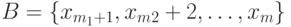 ,
, 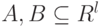 в – конечные множества в пространстве признаков;
в – конечные множества в пространстве признаков;  –
точки общего положения.
–
точки общего положения.
Определение. Точки  пространства
пространства 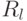 называются точками общего положения,
если никакая
называются точками общего положения,
если никакая  точка не лежит в гиперплоскости
размерности
точка не лежит в гиперплоскости
размерности  .
.
Приме р. Пусть  , т.е. рассматривается пространство
, т.е. рассматривается пространство  (плоскость).
Тогда точки
(плоскость).
Тогда точки  – точки общего положения, если никакие три из них не
лежат на одной прямой.
– точки общего положения, если никакие три из них не
лежат на одной прямой.
Теорема. Существует разделяющий комитет аффинных функционалов,
состоящий из не более, чем  членов при нечетном
членов при нечетном  и не более, чем
и не более, чем 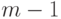 при четном
при четном  .
.
Доказательство. Рассмотрим случай 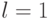 , т.е. пространство
, т.е. пространство 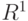 .
.
Пусть  ,
,  . Тогда возможны два случая.
. Тогда возможны два случая.
Для первого случая (рис. слева) функционал имеет вид:

Для второго случая (рис. справа) функционал имеет вид:

 – количество функционалов для худшего случая.
– количество функционалов для худшего случая.
Пусть  ,
,  . Тогда возможны следующие варианты.
. Тогда возможны следующие варианты.
Все случаи вида показанного на рис. слева сводятся к предыдущему  . Во всех остальных случаях функционалы надо располагать
аналогично рис. справа. Для худшего случая
. Во всех остальных случаях функционалы надо располагать
аналогично рис. справа. Для худшего случая  .
.
Пусть  (четное количество точек). Рассмотрим худший из возможных вариантов.
(четное количество точек). Рассмотрим худший из возможных вариантов.
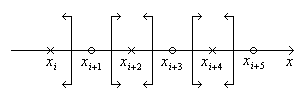
В данном случае функционалы надо располагать как показано на рис.  .
.
Пусть 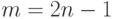 (нечетное количество точек). Рассмотрим худший из возможных вариантов.
(нечетное количество точек). Рассмотрим худший из возможных вариантов.
В данном случае функционалы надо располагать как показано на рис. 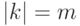 . Все остальные случаи можно свести либо к этим двум, либо к
предыдущим.
. Все остальные случаи можно свести либо к этим двум, либо к
предыдущим.
Таким образом, по методу математической индукции существует
разделяющий комитет аффинных функционалов из не более, чем  членов при нечетном
членов при нечетном  и не более, чем
и не более, чем 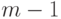 при четном
при четном  в пространстве
в пространстве 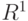 .
.
Многомерный случай сводится к одномерному следующим образом. Ищем
подпространство  такое, что
такое, что  ,
при
,
при 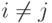 . Проектируем все
. Проектируем все  на
соответствующие подпространства, пока не получим одномерную задачу. В
многомерном случае для разделения
на
соответствующие подпространства, пока не получим одномерную задачу. В
многомерном случае для разделения  и
и  служит гиперплоскость:
служит гиперплоскость:
![(W,x)=\frac12\left[(W,x_i)+(W,x_j)\right]](/sites/default/files/tex_cache/12c6ec3cf1846108944566bb426ab69b.png)