Классификация на основе байесовской теории решений
2.4. Дискриминантные функции и поверхности решения
Минимизация риска и вероятности ошибки эквивалентны разделению
пространства признаков на  областей. Если области
областей. Если области 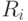 и
и 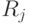 смежные, то
они разделены поверхностью решения в многомерном пространстве. Для
случая минимизации вероятности ошибки поверхность решения задается
уравнением:
смежные, то
они разделены поверхностью решения в многомерном пространстве. Для
случая минимизации вероятности ошибки поверхность решения задается
уравнением:


 монотонно возрастает.
монотонно возрастает.Определение. Функция 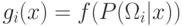 называется дискриминантной функцией.
называется дискриминантной функцией.
Таким образом, поверхность решения будет задаваться уравнением:
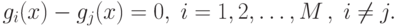
Для задачи классификации по вероятности ошибки или риску не всегда удается вычислить вероятности. В этом случае бывает более предпочтительно вычислить разделяющую поверхность на основе другой функции стоимости. Такие подходы дают решения, субоптимальные по отношению к Байесовской классификации.
2.5. Байесовский классификатор для нормального распределения
Распределение Гаусса очень широко используется по причине
вычислительного удобства и адекватности во многих случаях. Рассмотрим
многомерную плотность нормального распределения 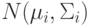 :
:
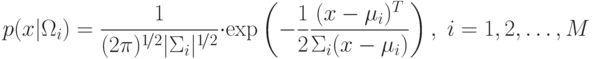
![\mu_i=E[X]](/sites/default/files/tex_cache/7f71ce38c2710ae6437629563825d352.png) – математическое ожидание случайной величины
– математическое ожидание случайной величины  в классе
в классе 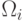 ,
, 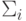 – матрица ковариации размерности
– матрица ковариации размерности  для класса
для класса 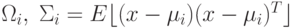 ,
,  – определитель матрицы ковариации.
Здесь
– определитель матрицы ковариации.
Здесь 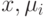 – это вектора-столбцы, а
– это вектора-столбцы, а 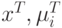 - вектора-строки.
- вектора-строки.5.1. Квадратичная поверхность решения. На основе этих данных необходимо построить байесовский классификатор. Рассмотрим логарифмическую дискриминантную функцию:
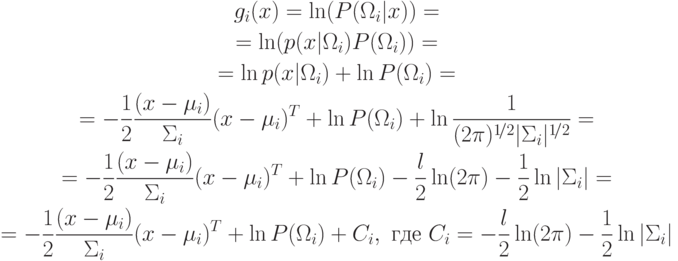
Эта функция представляет собой квадратичную форму. Следовательно,
разделяющая поверхность 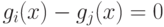 является гиперповерхностью второго порядка.
Поэтому Байесовский классификатор является квадратичным
классификатором.
является гиперповерхностью второго порядка.
Поэтому Байесовский классификатор является квадратичным
классификатором.
Пример. Пусть  .
Тогда
.
Тогда  .
.

Пример. Пусть



Т.к. 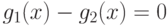 ,
то
,
то 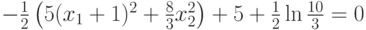

 .
.Пример. Пусть
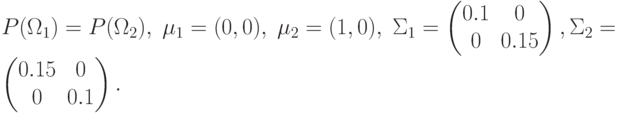

Из предыдущего примера:
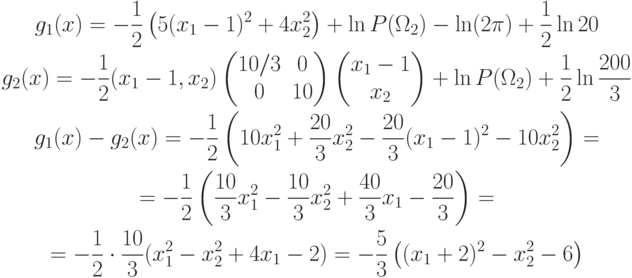
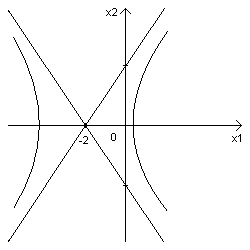
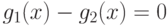 , то
, то 
 =6 – гипербола с центром в точке
=6 – гипербола с центром в точке 
5.2. Линейная поверхность решения. Условие остается тем же:

В предыдущем пункте мы получили квадратичную форму:
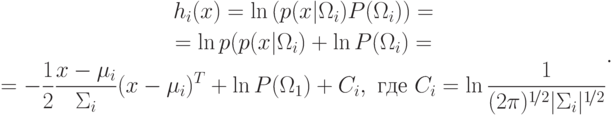
Пусть  , тогда
, тогда
![\begin{gathered}
h_i(x)=-\frac12\left[\frac{x}{\Sigma_i}x^T-\frac{\mu_i}{\Sigma_i}x^T-\frac{x}{\Sigma_i}\mu_i^T+\frac{\mu_i}{\Sigma_i}\mu_i^T\right]+\ln P(\Omega_i)+C_i= \\
=-\frac12\left[\frac{x}{\Sigma_i}x^T-2\frac{\mu_i}{\Sigma_i}x^T+\frac{\mu_i}{\Sigma_i}\mu_i^T\right]+\ln P(\Omega_i)+C_i=\\
=-\frac12\left[K_i(x)-2W_i x^T+W_i\mu_i^T\right]+\ln P(\Sigma_i)+C_i=\\
=-\frac12 K_i(x)+L_i(x)+C_i, \text{ где } L_i(x)=W_i x^T+W_{i0};\; W_i=\frac{\mu_i}{\Sigma_i};\\
W_{i0}=\ln P(\sigma_i\mu_i^T)
\end{gathered}](/sites/default/files/tex_cache/9360cf77b387fbeb987527ea3ed8a64c.png)
При  можно сравнивать только
можно сравнивать только  и
и 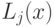 .
Таким образом, при
.
Таким образом, при  мы получили линейную поверхность решения.
мы получили линейную поверхность решения.
5.2.1. Линейная поверхность решения с диагональной матрицей ковариации.
Рассмотрим случай, когда матрица диагональная с одинаковыми элементами:  . Тогда
. Тогда  имеет вид:
имеет вид: 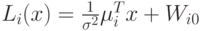 ;
;


 .
.Если  , то
, то  – это
середина вектора
– это
середина вектора  .
.
Т.к. 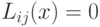 , то
, то 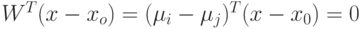 .
Следовательно, поверхность решения ортогональна
.
Следовательно, поверхность решения ортогональна 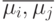 .
.
Пример. Рассмотрим пример разделяющей поверхности решения для
двухклассовой задачи с нормальным распределением. Поверхность решения
лежит ближе к 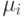 , если
, если  .
Соответственно, поверхность решения лежит
ближе к
.
Соответственно, поверхность решения лежит
ближе к  , если
, если 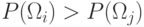 .
Также, если
.
Также, если  мало по отношению к
мало по отношению к 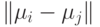 , то положение
поверхности решения не очень чувствительно к изменению
, то положение
поверхности решения не очень чувствительно к изменению 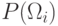 и
и  .
Последнее справедливо, т.к. вектора лежат в малых окрестностях
.
Последнее справедливо, т.к. вектора лежат в малых окрестностях 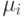 и
и  ,
поэтому изменение гиперплоскости их затрагивает не сильно. В центре
изображен случай малого, а справа случай большого
,
поэтому изменение гиперплоскости их затрагивает не сильно. В центре
изображен случай малого, а справа случай большого  .
.
5.2.2. Линейная поверхность решения с недиагональной матрицей ковариации. В этом случае уравнение:
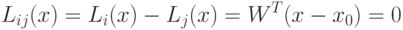
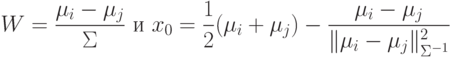
 норма
норма  ,
которая имеет вид:
,
которая имеет вид:  . Для такой нормы поверхность решения не
ортогональна вектору
. Для такой нормы поверхность решения не
ортогональна вектору  , Но она ортогональна его образу при преобразовании
, Но она ортогональна его образу при преобразовании 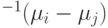 .
.