Математические методы распознавания образов
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 30.04.2008 | Доступ: свободный | Студентов: 1616 / 252 | Оценка: 4.24 / 3.92 | Длительность: 14:56:00
Тема: Компьютерная графика
Специальности: Математик
Теги: beta, IWR, recognition, алгоритмы, базисными векторами, выпуклая оболочка, выходной нейрон, направляющий вектор, обучение, поиск, полиэдр, пространство признаков, процедуры, разработка, сложность, собственный вектор, теория, эмпирический риск
Лекция 2:

Классификация на основе байесовской теории решений
A
|
версия для печати
< Лекция 1 || Лекция 2: 12345 || Лекция 3 >

2.2. Ошибка классификации

Определение. Вероятность P_e=P(x\in R_2,\Omega_1)+P(x\in R_1,\Omega_2) называется ошибкой классификации,

R_1=\{x:P(\Omega_1)p(x|\Omega_1)>P(\Omega_2)p(x|\Omega_2)\}, \; R_2=\{x:P(\Omega_1)p(x|\Omega_1)<P(\Omega_2)p(x|\Omega_2)\}
– области решения (\Omega_1\cap\Omega_2=\oslash).

Теорема. Байесовский классификатор является оптимальным по отношению к минимизации вероятности ошибки классификации.

Доказательство. Рассмотрим ошибку классификации:

\begin{gathered} P_e=P(x\in R_2,\Omega_1)+P(x\in R_1,\Omega_2)= \\ = P(\Omega_1)\int_{R_2}p(x|\Omega_1)dx+P(\Omega_2)\int_{R_1}p(x|\Omega_2)dx = \\ = P(\Omega_1)\left( 1-\int_{R_1}p(x|\Omega_1)dx\right)+P(\Omega_2)\int_{R_1}p(x|\Omega_2)dx = \\ = P(\Omega_1)-P(\Omega_1)\int_{R_1}p(x|\Omega_1)dx+P(\Omega_2)\int_{R_1}p(x|\Omega_2)dx = \end{gathered}

Учитывая формулу Байеса:

p(x|\Omega_i)=\frac{P(\Omega_i|x)p(x)}{P(\Omega_i)}, \; i=1,2,
получим:
\begin{gathered} =P(\Omega_1)-P(\Omega_1)\int_{R_1}\frac{P(\Omega_1|x)p(x)}{P(\Omega_1)}dx+P(\Omega_2)\int_{R_1}\frac{P(\Omega_2|x)p(x)}{P(\Omega_2)}dx = \\ =P(\Omega_1)-\int_{R_1}P(\Omega_1|x)p(x)dx+\int_{R_1}P(\Omega_2|x)p(x)dx =\\ =P(\Omega_1)-\int_{R_1}p(x)(P(\Omega_1|x)-P(\Omega_2|x))dx \end{gathered}
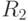Таким образом, минимум достигается, когда R_1=\{ x:P(\Omega_1|x)>P(\Omega_2|x)\}. R_2 выбирается из остальных точек.

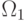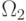Данная теорема была доказана для двух классов \Omega_1 и \Omega_2. Обобщим ее на M классов.

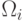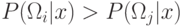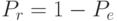Пусть вектор признаков x относится к классу \Omega_i, если P(\Omega_i|x)>P(\Omega_j|x), при i\neqj, \; i=1,2,\ldots,M, \; j=1,2,\ldots,M. Соответственно необходимо доказать, что данное правило минимизирует вероятность ошибки классификации. Для доказательства следует воспользоваться формулой правильной классификации P_r=1-P_e.

Доказательство. Воспользуемся формулой правильной классификации 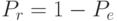P_r=1-P_e.

\begin{gathered} P_r=P(x\in R_1,\Omega_1)+P(x\in R_2,\Omega_2)+\ldots+P(x\in R_i,\Omega_i)= \\ =\sum_{i=1}^l P(x\in R_i|\Omega_i)P(\Omega_i)= \\ =\sum_{i=1}^l P(\Omega_i)\int\limits_{R_i}p(x|\Omega_i)dx= \\ =P(\Omega_1)\left(1-\sum_{i=2}^l\int\limits_{R_i}p(x|\Omega_1)dx \right)+\sum_{i=2}^l P(\Omega_i)\int\limits_{R_i}p(x|\Omega_i)dx= \\ =P(\Omega_1)-\sum_{i=2}^l\left[P(\Omega_1)\int\limits_{R_i}p(x|\Omega_1)dx-P(\Omega_i)\int\limits_{R_i}p(x|\Omega_i)dx\right]= \end{gathered}
Учитывая формулу Байеса: p(x|\Omega_i)=\frac{P(\Omega_i|x)p(x)}{P(\Omega_i)}, \; i=1,2,\ldots,l, получим:
\begin{gathered} =P(\Omega_1)-\sum_{i=2}^l\left[P(\Omega_1)\int\limits_{R_i}\frac{P(\Omega_1|x)p(x)}{P(\Omega_1)}dx- P(\Omega_1)\int\limits_{R_i}\frac{P(\Omega_i|x)p(x)}{P(\Omega_i)}dx\right]=\\ =P(\Omega_1)-\sum_{i=2}^l\left[\int\limits_{R_i}P(\Omega_1|x)p(x)dx-\int\limits_{R_i}P(\Omega_1|x)p(x)dx\right]=\\ =P(\Omega_1)-\sum_{i=2}^l\int\limits_{R_i}p(x)\left[P(\Omega_1|x)-P(\Omega_i|x) \right]dx \end{gathered}
Таким образом, максимум достигается, когда P(\omega_1|x)<P(\omega_i|x). Аналогично для всех j=1,2,\ldots,l максимум достигается, когда R_i=\{x:P(\omega_j|x)<P(\omega_i|x)\}.

Дальше >>
< Лекция 1 || Лекция 2: 12345 || Лекция 3 >

Вопросы и ответы

вопросов: 0