Задача распознавания образов

1.3. Классификация с обучением и без обучения

В зависимости от наличия или отсутствия прецедентной информации различают задачи распознавания с обучением и без обучения. Задача распознавания на основе имеющегося множества прецедентов называется классификацией с обучением (или с учителем).

Рис. 1.4. Изображение различных типов поверхности и кластеризация соответствующих векторов признаков

В том случае, если имеется множество векторов признаков, полученных для некоторого набора образов, но правильная классификация этих образов неизвестна, возникает задача разделения этих образов на классы по сходству соответствующих векторов признаков. Эта задача называется кластеризацией или распознаванием без обучения.

Пример 2. Рассмотрим съемку со спутника и классификацию поверхности по отраженной энергии (рис.1.4). На рисунке изображены снимок из космоса (слева) и результат кластеризации векторов признаков, рассчитанных для различных элементов изображения (справа). Распределение образов, изображенных точками ( ) по классам осуществляется на основе анализа "скоплений" этих точек в пространстве признаков.

Пример 3. Рассмотрим другой пример распознавания образов – в общественных (социальных) науках. Целью задачи является построение системы классификации государств для определения необходимости гуманитарной поддержки со стороны международных организаций. Необходимо выявить закономерности связей между различными, объективно измеряемыми параметрами, например, связь между ВНП, уровнем грамотности и уровнем детской смертности. В данном случае страны можно представить трехмерными векторами, а задача заключается в построении меры сходства этих векторов и дальнейшем построении схемы кластеризации (выбора групп) по этой мере.

1.4. Формальная постановка задачи классификации

Будем использовать следующую модель задачи классификации.

- множество объектов распознавания (пространство образов).

- объект распознавания (образ).

- индикаторная функция, разбивающая пространство образов на непересекающихся классов . Индикаторная функция неизвестна наблюдателю.

– пространство наблюдений, воспринимаемых наблюдателем (пространство признаков).

- функция, ставящая в соответствие каждому объекту точку 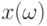в пространстве признаков. Вектор 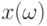- это образ объекта, воспринимаемый наблюдателем. В пространстве признаков определены непересекающиеся множества точек , соответствующих образам одного класса.

- решающее правило – оценка для 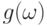на основании 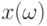, т.е. .

Пусть – доступная наблюдателю информация о функциях 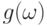и 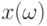, но сами эти функции наблюдателю неизвестны. Тогда – есть множество прецедентов.

Задача заключается в построении такого решающего правила 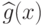, чтобы распознавание проводилось с минимальным числом ошибок.

Обычный случай – считать пространство признаков евклидовым, т.е. . Качество решающего правила измеряют частотой появления правильных решений. Обычно его оценивают, наделяя множество объектов некоторой вероятностной мерой. Тогда задача записывается в виде .