Представление графической информации
Таким образом, B-сплайн второй степени для точек 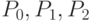 и
и  с узловым вектором (0, 0, 0, 1, 3, 3, 3) определяется в виде
с узловым вектором (0, 0, 0, 1, 3, 3, 3) определяется в виде
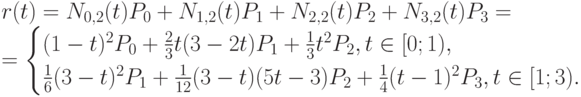
На рис. 3.26 показан квадратичный B-сплайн, который построен по приведенной выше формуле для 4 точек, отмеченных на рисунке.
Различные виды B-сплайнов определяются узловыми векторами. В 3D-графике используются также сплайн-поверхности.
Фракталы
Во фрактальной графике изображение строится по специальным формулам или алгоритмам. Фрактальные графические редакторы позволяют получать сложные и реалистичные изображения.
Ниже рассматриваются примеры построения различных видов фракталов - геометрических, с помощью описания L-систем (п. 3.3.1) и векторного предста
Черепашья графика. L-системы
Фрактал - это множество, которое обладает свойством самоподобия. Ограниченная геометрическая фигура называется самоподобной, если она составлена из некоторого набора частей, каждая из которых конгруэнтна фигуре, подобной всей фигуре с некоторым коэффициентом подобия. Если этот коэффициент одинаков для всех частей и количество этих частей равно n, то говорят, что данная фигура самоподобна относительно этого коэффициента и данного n. Если коэффициенты для разных частей могут быть различными, то фигура называется самоподобной относительно соответствующего набора коэффициентов.
Одним из способов построения самоподобных геометрических фигуры является использование черепашьей графики.
Черепашья графика - способ конструирования графических изображений с помощью рисующей черепахи. Черепаха - это метафора, или некоторый воображаемый объект, который оставляет след при движении по экрану, аналогичный следу черепахи на песке. Рисующая черепаха умеет выполнять следующие действия: идти вперед на заданное число шагов, поворачиваться налево или направо на заданный угол, поднимать или опускать перо, так чтобы она могла перемещаться, оставляя или не оставляя след (оказываться в заданной точке).
Примером описания геометрических объектов, которые строятся с помощью рисующей черепахи, являются L-системы. Понятие L-системы было введено биологом Аристидом Линденмайером (1968) [11]. Фигура описывается в виде слова, заданного в некотором алфавите в соответствии с определенной грамматикой. Каждая буква алфавита соответствует некоторому действию рисующей черепахи. Поэтому данное слово определяет и саму процедуру построения изображения фигуры с помощью черепашьей графики.
Рассмотрим следующий алфавит:
- F - смещение на заданный интервал с оставлением следа;
- f - смещение на заданный интервал без следа;
- + - поворот на заданный угол направо;
- - - поворот на заданный угол налево;
- [ - начало записи действий в стек;
- ] - окончание записи действий в стек;
- X - вспомогательный символ.
Например, квадрат можно представить в виде слова F+F+F+F, где угол поворота - прямой (рис. 3.27 (a)), а правильный треугольник - в виде слова F+F+F, где угол поворота равен  (рис. 3.27 (b)).
(рис. 3.27 (b)).
Символу X соответствует "пустое" действие рисующей черепахи, он используется только для формулирования правил. После выполнения действий, записанных в стек, черепаха оказывается там же, где была.
Описание фигуры в виде L-системы состоит в определении аксиомы - начального символа грамматики, правил грамматики и величины угла поворота. При построении фигуры указывается также величина смещения и число применения множества правил грамматики к словам, полученным на предыдущих итерациях. Кроме того, для практической реализации требуется задать начальное местоположение черепахи и ее направление (например, начальный угол направления движения относительно оси абсцисс).
Если в виде L-системы описывается фрактал, то для построения его приближения, указывается также число итераций  , а сам фрактал получается в пределе при
, а сам фрактал получается в пределе при 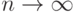 . Нулевая итерация соответствует аксиоме. Приближения фрактала называются фрактальными фигурами.
. Нулевая итерация соответствует аксиоме. Приближения фрактала называются фрактальными фигурами.
Пример 25. Рассмотрим описание в виде L-системы кривой Коха:
угол:  ;
;
аксиома: F;
правило: 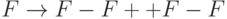 .
.
Шаг итерации состоит в замене каждого символа F в слове, полученном на предыдущем шаге, на строку F-F++F-F.
Пусть 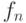 - кривая, полученная на шаге n, для
- кривая, полученная на шаге n, для  . Кривая Коха является пределом последовательности
. Кривая Коха является пределом последовательности  при
при 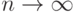 . Это непрерывная кривая, которая не имеет касательной ни в одной точке. Элемент
. Это непрерывная кривая, которая не имеет касательной ни в одной точке. Элемент 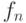 называется n-м приближением кривой Коха (рис. 3.28).
называется n-м приближением кривой Коха (рис. 3.28).
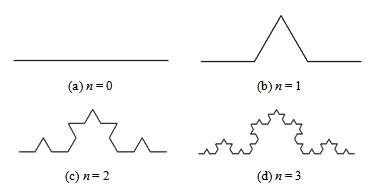
Рассмотрим первые 3 приближения кривой Коха. Кривая  соответствует аксиоме F и представляет собой отрезок ( рис. 3.28 (a)). Кривая
соответствует аксиоме F и представляет собой отрезок ( рис. 3.28 (a)). Кривая 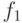 соответствует слову F-F++F-F (рис. 3.28 (b)), кривая
соответствует слову F-F++F-F (рис. 3.28 (b)), кривая  - слову
- слову
F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F
(рис. 3.28 (c)), кривая 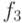 показана на рис. 3.28 (d).
показана на рис. 3.28 (d).
Пусть 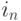 - число отрезков, содержащихся в фигуре
- число отрезков, содержащихся в фигуре 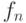 , и
, и 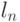 -длина слова, описывающего фигуру на шаге n, т. е. число символов, которое содержит это слово. В соответствии с грамматикой имеем:
-длина слова, описывающего фигуру на шаге n, т. е. число символов, которое содержит это слово. В соответствии с грамматикой имеем:
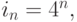 для
для 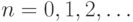 ;
; 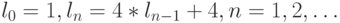
Из приведенного выше рекуррентного соотношения получаем, что

для