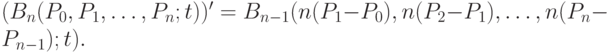Представление графической информации
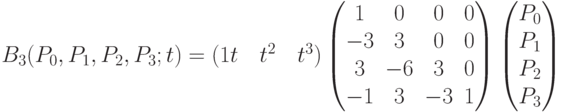
В общем случае столбец j матрицы порядка n + 1 кривой Безье 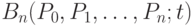 образуют коэффициенты при
образуют коэффициенты при  полинома
полинома 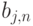 .
.
Найдем значения производной кривой Безье в точках 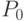 и
и 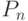 . Для n > 0 и
. Для n > 0 и ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png) имеем (см. ниже утверждение 3):
имеем (см. ниже утверждение 3):
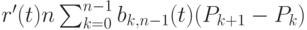
Следовательно, 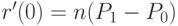 и
и 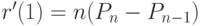 .
.
Производная в точке 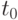 , если существует, находится в виде:
, если существует, находится в виде:  . Поэтому
. Поэтому  , если
, если  , и
, и 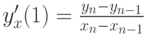 , если
, если 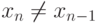 . Таким образом, кривая Безье касается в точке
. Таким образом, кривая Безье касается в точке 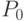 отрезка
отрезка ![[P_0; P_1]](/sites/default/files/tex_cache/68882d832181786921dae7f283d6bae7.png) , а в точке
, а в точке 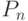 - отрезка
- отрезка ![[P_n; P_{n - 1}]](/sites/default/files/tex_cache/e16a4ea34454451180ed9a51eef2a7d9.png) .
.
Выпуклым называется множество, содержащее для любой пары его точек A и B все точки отрезка, соединяющего точки A и B. Выпуклой оболочкой множества точек является наименьшее выпуклое множество, содержащее эти точки.
Утверждение 1. Для  выполняется соотношение
выполняется соотношение
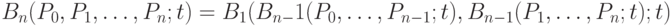
Доказательство. Имеем:
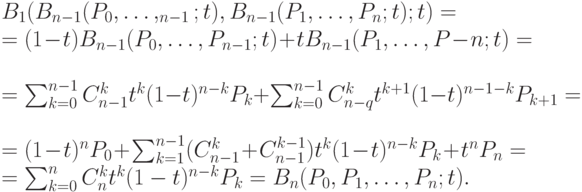
Из утверждения 1 следует, что кривая Безье не выходит за пределы выпуклой оболочки точек  .
.
Утверждение 2. Для  имеет место равенство:
имеет место равенство:

Доказательство. Имеем:
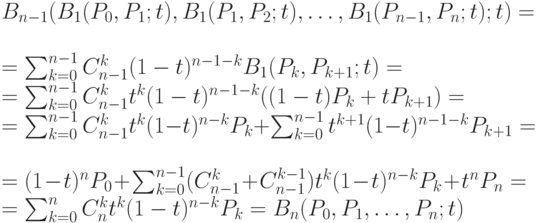
На утверждении 2 основан метод приближенного построения кривых Безье, созданный Полем де Кастельжо, еще одним изобретателем этих кривых (1959). Например, из утверждения 2 следует, что точка кривой Безье порядка n, соответствующая t = 0,5, совпадает при t = 0,5 с точкой кривой Безье порядка n - 1, построенной по точкам 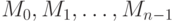 , которые являются серединами отрезков, соединяющих точки
, которые являются серединами отрезков, соединяющих точки 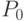 и
и 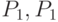 и
и 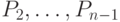 и
и 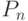 , соответственно.
, соответственно.
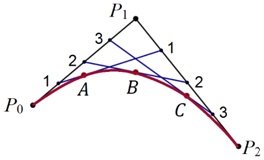
Пример 17. Рассмотрим точки A, B, и C квадратичной кривой Безье, построенной в примере 16 (см. рис. 3.20), соответствующие значениям 0,25, 0,5 и 0,75 параметра t. По утверждению 2,
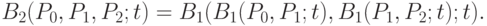
Кривыми Безье первого порядка, построенными по точкам 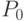 и
и  , а также
, а также  и
и  , являются соответственно отрезки
, являются соответственно отрезки  и
и  ( рис. 3.20). Значениям 0,25, 0,5 и 0,75 параметра t на них соответствуют точки
( рис. 3.20). Значениям 0,25, 0,5 и 0,75 параметра t на них соответствуют точки 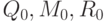 и
и 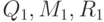 , которые делят эти отрезки на 4 равные части. Имеем:
, которые делят эти отрезки на 4 равные части. Имеем:
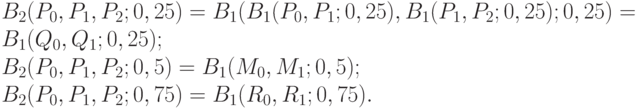
Следовательно, точка A квадратичной кривой Безье совпадает с точкой отрезка  , которая отстоит на четверть от его конца
, которая отстоит на четверть от его конца 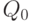 , точка B - с серединой отрезка
, точка B - с серединой отрезка 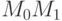 и точка C - с точкой отрезка
и точка C - с точкой отрезка  , отстоящей на три четверти от его конца
, отстоящей на три четверти от его конца 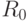 .
.
Рассмотрим примеры приближенного построения кривых Безье. Будем использовать 3 вспомогательные точки, которые соответствуют значениям 0,25, 0,5 и 0,75 параметра t.
Пример 18. Построим кривую Безье по 3 точкам 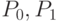 и
и  . Соединим отрезками точки
. Соединим отрезками точки 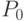 и
и  , а также
, а также  и
и  , и разделим каждый отрезок на 4 равные части, отметив на них по 3 точки - концы этих частей. Занумеруем эти точки так, как показано на 3.21рис..
, и разделим каждый отрезок на 4 равные части, отметив на них по 3 точки - концы этих частей. Занумеруем эти точки так, как показано на 3.21рис..
Соединим отрезками точки с равными номерами и отметим на первом из них точку A, отстоящую на четверть от первого конца отрезка, на втором - середину B и на третьем отрезке - точку C, отстоящую на три четверти от первого его конца.
Теперь проведем кривую, которая проходит через точки 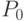 , A, B, C и
, A, B, C и  так, чтобы она касалась построенных отрезков и не выходила за их пределы, как показано на рисунке 3.21.
так, чтобы она касалась построенных отрезков и не выходила за их пределы, как показано на рисунке 3.21.
Пример 19. Построим кривую Безье по 4 точкам 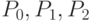 и
и  , как показано на рис. 3.22. Как и ранее, соединим точки
, как показано на рис. 3.22. Как и ранее, соединим точки 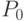 и
и 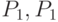 и
и 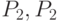 и
и  отрезками и разделим каждый отрезок на 4 равные части, занумеровав точки деления так, как показано на рисунке. Последовательно соединим отрезками точки с равными номерами.
отрезками и разделим каждый отрезок на 4 равные части, занумеровав точки деления так, как показано на рисунке. Последовательно соединим отрезками точки с равными номерами.
На первой паре отрезков отметим точки, отстоящие от первого конца отрезка на четверть, соединим их и на новом отрезке отметим точку A, отстоящую на четверть от первого конца отрезка. Точно так же, соединим середины второй пары отрезков и на новом отрезке отметим середину B. На третьей паре отрезков отметим точки, отстоящие от начала на три четверти, соединим их и на новом отрезке отметим точку C, отстоящую на три четверти от первого его конца.
Проведем кривую, которая проходит через точки 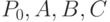 и
и  и касается в них построенных отрезков, но не выходит за их пределы.
и касается в них построенных отрезков, но не выходит за их пределы.
Утверждение 3. Для n > 0 и ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png) выполняется соотношение
выполняется соотношение
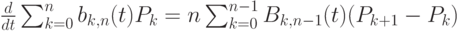
Доказательство. Имеем:

так как 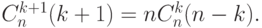
Следствие. Для n > 1 является верным равенство