Представление графической информации
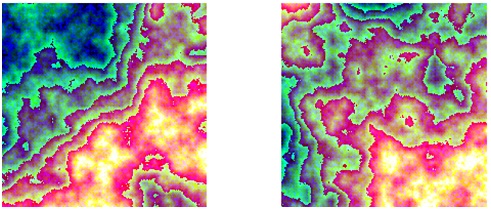
Фрактал "Плазма"
Построение фрактала "Плазма" зависит от случайных параметров. Оно сводится к раскрашиванию прямоугольника по некоторому правилу.
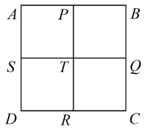
Пусть I - множество номеров цветов из некоторой палитры, такое что I = {0, 1, 2, ..., N}, и ABCD - прямоугольник. Обозначим через M множество пикселей прямоугольника ABCD (рис. 3.39).
Пусть 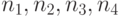 - четыре попарно различные элемента множества I. Раскрасим в цвета с этими номерами вершины A, B, C и D, соответственно (рис. 3.40).
- четыре попарно различные элемента множества I. Раскрасим в цвета с этими номерами вершины A, B, C и D, соответственно (рис. 3.40).
Обозначим через T точку пересечения диагоналей прямоугольника ABCD и раскрасим ее в цвет с номером n, где  .
.
Пусть P, Q, R и S - середины сторон AB, BC, CD и DA, соответственно. Обозначим через  - длину стороны XY. Для точки P положим
- длину стороны XY. Для точки P положим
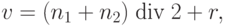
где r - случайное целое число, такое что 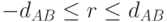 .
.
Раскрасим точку P в цвет с номером m, где

Аналогично находятся номера цветов для точек Q, R и S.
Иногда слагаемое r в соотношение для v добавляется не для каждой стороны, а только для одной из них. Случайное число также может участвовать в определении цвета центра квадрата.
Описанная выше процедура применяется к прямоугольникам APTS, PBQT, TQCR и STRD (см.рис. 3.39). Далее построение продолжается рекурсивно до тех пор, пока не будет найден цвет для каждого пикселя множества M.
На рис. 3.40 приведены два варианта раскраски квадрата по описанному выше методу. Попарно различные цвета вершин квадрата выбираются случайным образом. Палитра состоит из 216 "безопасных" цветов.
Кодирование звуковой информации
В природе звуковые сигналы имеют непрерывный спектр частот, т. е. являются аналоговыми. Для записи и воспроизведения звука используются методы дискретизации и квантования. Основными параметрами звуковых волн являются частота и амплитуда колебаний. Частоту измеряют в герцах (в музыке ее называют тоном). Амплитуда звуковых колебаний характеризует громкость звука, ее называют силой звука или его давлением, она измеряется в паскалях. Из-за большого разброса значений используют логарифмическую шкалу децибелов как показателей уровня звука. Основными методами кодирования звука являются
- метод частотной модуляции FM (frequency modulation);
- метод таблично-волнового синтеза (wave table).
В методе частотной модуляции используется разложение звуковой волны на синусоиды, описывающие базовые колебания (гармоники). Разложение на последовательность гармонических сигналов и представление в виде дискретных цифровых сигналов (двоичных кодов) осуществляется с помощью специальных устройств - аналого-цифровых преобразователей. Обратное преобразование и воспроизведение звука, закодированного числовым кодом, выполняют цифро-аналоговые преобразователи. Недостатком данного метода является то, что при преобразованиях неизбежны потери информации, поэтому качество звучания не всегда получается удовлетворительным.
При использовании метода таблично-волнового синтеза образцы множества различных звуков хранятся в заранее подготовленных таблицах. Числовые коды этих образцов содержат параметры, характеризующие особенности звука. Качество звука получается высокое, оно приближается к качеству звучания реальных музыкальных инструментов (подробнее о представлении звуковой информации в компьютере.).
Упражнения
-
Определите примерный тон, а также светлый он или темный, только по его компонентам для цвета
a) rgb(50, 50, 50) ;
b) rgb(90, 0, 100) ;
c) rgb(150, 200, 140) .
-
Найдите 1) 16-ричный код; 2) двоичный код; 3) ближайший "безопасный цвет" для цвета
a) rgb(101, 202, 55) ;
b) rgb(236, 12, 133) ;
c) rgb(17, 135, 250) .
-
Найдите целые RGB-компоненты цвета
a) f073ab;
b) 5d5d5d;
c) ссff33 (hex) .
-
Найдите цветовые компоненты в модели CMYK цвета
a) rgb(0,9, 0.4, 0,7)
b) rgb(24, 108, 209) ;
c) hsv(350, 90, 70) .
-
Найдите цветовые компоненты в модели HSV цвета
a) rgb(0,6, 0.8, 0,25) ;
b) rgb(105, 244, 56) ;
c) cmyk(0,4, 0,8, 0, 0,5) .
-
Найдите цветовые компоненты в модели RGB цвета:
a) cmyk(0,25, 0, 0,85, 0,7) ;
b) cmyk(0, 0,33, 0,88, 0,25) ;
c) hsv(100, 50, 80) ;
d) hsv(240, 100, 40).
-
Постройте черно-белое пиксельное изображение, каждая строка которого закодирована двоичным словом, в котором 0 соответствует белому цвету, а 1 - черному, если его код (hex) имеет вид:
a) 1830 0c60 4aa4 76dc 2aa8 1c70 0000 1c70 2aa8 76dc 4aa4 0c60 1830;
b) 3e 42 02 44 10;
c) 3f 41 01 42 18
d) 31 6b a5 6b 31.
- Придумайте свой способ символьных изображений букв и цифр, например, с помощью символов (U+2591) и (U+2588) в виде
-
Найдите параметрическое представление кривой Безье для точек c координатами
a) (0; 0); (5; 5); (6;1);
b) (- 2; 0); (- 1; 1); (0; 0); (2; 0).
-
Постройте приближенно кривую Безье для точек, взаимное расположение которых показано на рис. 3.41, по методу Кастельжо.
- Постройте кривые Безье для точек с взаимным расположением, приведенным на рис. 3.41 (b-e), в графическом редакторе Paint.
- Найдите матричное представление кривой Безье 4-го порядка.
- Составьте общее уравнение годографа кривой Безье 2-го порядка.
-
Постройте в системе координат
 для узлового вектора
для узлового вектораa) (0, 1, 2, 3, 4);
b) (0, 0, 1, 3, 4).
-
Найдите параметрическое представление B-сплайна для n точек и k узлов, если узловой вектор имеет вид:
a) (0, 0, 1, 3, 3), n = 2, k = 1; b) (0, 1, 2, 3, 4, 5, 6, 7), n = 4, k = 2;
a) (0, 0, 0, 1, 1, 1), n = k = 2; b) (0, 0, 0, 0, 1, 3, 5, 5, 5, 5), n = 5, k = 3.
-
Найдите число отрезков, из которых состоит приближенное изображение фрактала "дерево", после выполнения n итераций.
Найдите размерность подобия для салфетки Серпинского.
Опишите в виде L-системы и выполните построение для первых двух итераций
a) снежинки Коха;
b) квадратичного острова Коха;
c) кривой Гильберта.
-
Постройте фигуру, которая получается после первой и второй итераций, если в виде L-системы ее описание имеет вид (рис. 3.42):
a)угол:
 ; аксиома: F; правило:
; аксиома: F; правило: ![F \to F[+F][-F]F](/sites/default/files/tex_cache/05e99e9cb9a705eb325f200e791c6f0e.png) ;
;b)угол:
 ; аксиома: F; правило:
; аксиома: F; правило: ![F \to -F+F+[+F-F-]-[-F+F+F]](/sites/default/files/tex_cache/11aed6fe1aec651431caa115b40f0c27.png) ;
;c)угол:
 ; аксиома: F; правило:
; аксиома: F; правило: ![F \to -F[-F+F-F]+[+F-F-F]](/sites/default/files/tex_cache/11660bea5fca092f0be7718a0dda4209.png) ;
;d)угол:
 ; аксиома: F; правило:
; аксиома: F; правило: ![F \to F[+F][-F][F]](/sites/default/files/tex_cache/471e13d723a67a3cbd9d94454cdf34db.png) .
.На рис. 3.44 фигуры (a-c) показаны после четырех, а фигура (d) - после шести итераций.
- Постройте в графическом редакторе Paint изображение снежинки Коха для первых двух итераций, с помощью графических примитивов и преобразований наклона, поворота и отражения.
-
Добавим в алфавит грамматики L-системы коэффициент q, обозначающий изменение длины отрезка смещения в q раз. Фрактал дерево Пифагора (рис. 3.43) в виде L-системы можно описать в виде:
угол:
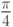 ; аксиома: F--X; коэффициент q:
; аксиома: F--X; коэффициент q: ;
;правила:
![F \to qF, X \to qF[+X][-F[X]--F]--qF-qF](/sites/default/files/tex_cache/d2772aacceda496f8571cf706169de31.png) .
.Постройте фрактал дерево Пифагора для первых 3 итераций.
-
Опишите в виде L-системы фрактал "двоичное дерево" (рис. 3.44).
Указание. Возьмите в качестве аксиомы слово FX.