Представление графической информации

Положим 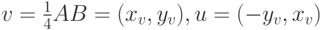. Тогда радиус-векторы вершин ломаной находятся следующим образом:

OC = OA + v; OD = OC + u; OE = OD + v; OF = OC + v;
OG = OF - u; OH = OG + v; OI = OF + v. 

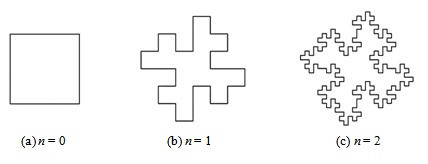
На рис. 3.34 показаны первые 2 итерации построения фигуры.

Рис. 3.34. Четверичный остров Коха, первые 2 итерации

Пример 30. Рассмотрим фрактал, который называется кривой Гильберта. Кривая Гильберта представляет собой непрерывную кривую, которая полностью заполняет квадрат. Она являет

Рис. 3.35. Кривая Гильберта, первые 4 итерации

Построим векторное представление ломаной на шаге итерации n, для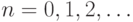

Пусть M - точка и 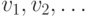- векторы. Обозначим через 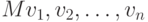ломаную, первой вершиной которой является точка M, следующая вершина является концом вектора 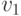, отложенного от точки M, третьей вершиной является конец вектора 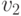, отложенного от второй вершины ломаной, и так далее.

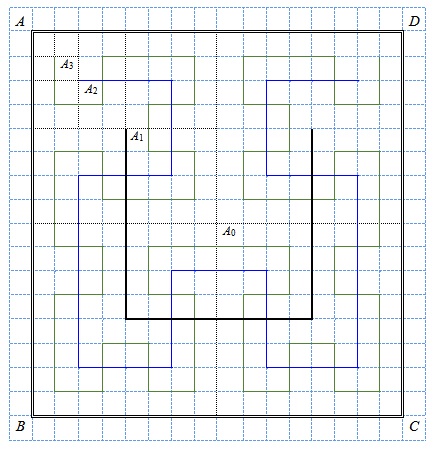
Ломаную 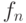можно построить с помощью последовательности векторов, параллельных сторонам квадрата и имеющих одинаковую длину. Пусть ABCD - квадрат (рис. 3.36). Положим . На каждом шаге длина векторов, составляющих ломаную, уменьшается вдвое. Обозначим , для

Рис. 3.36. Построение кривой Гильберта

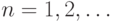
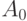Ломаная состоит из вершины , являющейся серединой диагонали AC, и пустой последовательности векторов. Ломаная 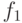имеет вид 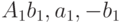(см. рис. 3.36), где точка 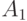- середина отрезка .

Ломаная выглядит следующим образом:

где точка 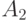является серединой отрезка .

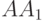Обозначим через 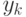произвольную подпоследовательность векторов ломаной . Через ( ) обозначим последовательность векторов, которая получается из последовательности 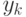заменой каждого вектора на противоположный к нему вектор. Далее, обозначим через 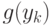последовательность векторов, которая получается из последовательности 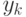одновременной заменой всех вхождений вектора 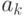на вектор 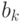, а вектора 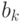- на вектор 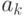. Кроме того, обозначим через 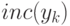последовательность векторов, которая отличается от последовательности 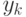заменой всех индексов на k + 1.

Пусть теперь 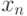- последовательность векторов ломаной 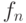. Имеем:

- пустая последовательность;

для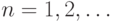

Обозначим через 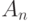точку, от которой откладывается последовательность векторов 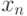, для 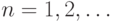Очевидно, что точки 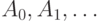лежат на диагонали AC квадрата (см. рис. 3.36) и удовлетворяют соотношениям:

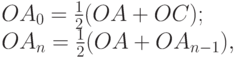
для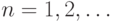

Множество Мандельброта

Рассмотрим фрактал множество Мандельброта (рис. 3.37).

Рис. 3.37. Множество Мандельброта

Пусть 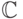- множество комплексных чисел и D - множество точек квадрата [- 2; 2] x [- 2; 2], так что

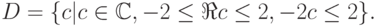
Для каждой точки c из множества D рассмотрим отображение , такое что 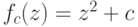. Множество Мандельброта состоит из таких точек c множества D, для которых траектория точки 0 при отображении 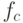не выходит за пределы круга радиуса 2, т. е. для каждой точки z множества

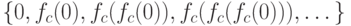
выполняется условие: | z | < 2. Указанное множество представляет собой последовательность точек 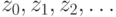, таких что

для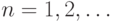

Положим 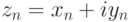, для 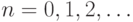, и c = x + iy. Тогда из данного соотношения будем иметь:

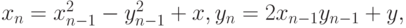
для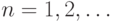

Нулевая итерация соответствует множеству D. После первой итерации остаются точки, лежащие в круге радиуса 2, т. е. такие точки c, что | c | < 2, или 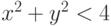. После второй итерации остаются точки c, для которых выполняется условие 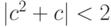(рис. 3.38), и т. д.

Рис. 3.38. Множество Мандельброта, 512 итераций

На рис. 3.38 черным цветом выделено множество точек, которые остаются в круге радиуса 2 после 512 итераций. Точки, которые выходят за пределы этого круга на разных шагах итерации, отличаются цветом.