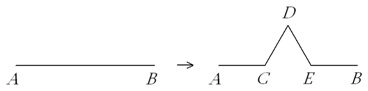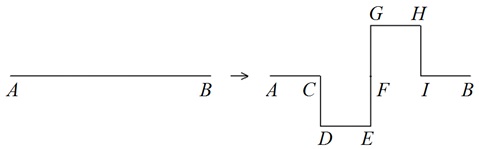Представление графической информации

Например, фигура, полученная на шаге 4, состоит из 256 отрезков, а описывающая ее строка - из 596 символов.

Если фигуру можно разбить на N частей, каждая из которых может быть получена из целой фигуры, конгруэнтной исходной, преобразованием подобия с коэффициентом r, то размерность подобия D фигуры удовлетворяет соотношению 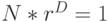, и, следовательно,

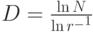
Найдем, например, размерность подобия кривой Коха. На каждом шаге итерации фигуру можно разбить на 4 части, каждая из которых конгруэнтна фигуре, подобной всей фигуре, полученной на предыдущем шаге, с коэффициентом подобия . Поэтому размерность подобия кривой Коха находится следующим образом:

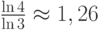
В общем случае размерность подобия фрактальных фигур, в отличие от "обычных", также не является целым числом. Разобьем, например, отрезок на n равных частей, где n > 0. Каждая часть подобна исходной фигуре с коэффициентом подобия 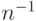. Поэтому размерность подобия отрезка равна 1. Аналогично, разобьем квадрат на n одинаковых квадратов. Тогда для некоторого натурального k. При этом каждый из n квадратов будет подобен исходному квадрату с коэффициентом подобия 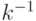. Поэтому размерность подобия квадрата равна .

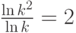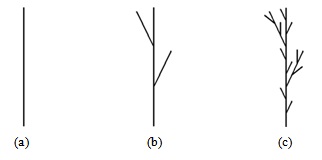
Пример 26. Рассмотрим фрактал "дерево" (рис. 3.29). Его описание в виде L-системы имеет вид:

угол:

аксиома: F;

правило: F -> F[+F]F[-F]F.

На первом шаге итерации сначала проводится отрезок заданной длины; затем выполняются действия, описанные в квадратных скобках, т. е. в "стеке" - делается поворот направо на угол и проводится еще один отрезок; после этого черепаха возвращается в положение, которое у нее было перед "стеком", и проводится следующий отрезок; затем выполняется поворот налево на угол и снова проводится отрезок; после этого черепаха возвращается к положению перед последним "стеком" и проводится еще один отрезок. На рис. 3.29 показаны результаты построения дерева на нулевом (a), первом (b) и втором (c) шагах итерации.

Рис. 3.29. Дерево. Итерация (a) 0; (b) 1; (c) 2

Фрактал "дерево" получается при неограниченном увеличении числа итераций. Размерность подобия для него имеет вид:

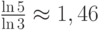
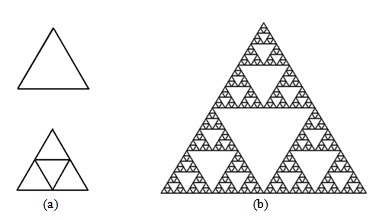
Пример 27. Рассмотрим описание в виде L-системы еще одного хорошо известного фрактала - салфетки Серпинского (рис. 3.30). Имеем:

угол: ;

аксиома: FXF--FF-FF;

правила:

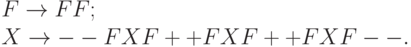
На рис. 3.30 показаны фигуры, соответствующие нулевой, первой и пятой итерациям.

Рис. 3.30. Салфетка Серпинского. Итерация (a) 0 (вверху) и 1; (b) 5

Острова Коха и кривая Гильберта

Рассмотрим примеры представления фракталов с помощью геометрического описания преобразования отрезка на шаге итерации. Иногда указывается преобразование не для отрезка, а для ломаной, как при построении кривой Гильберта (см. ниже).

Пример 28. Построим два троичных острова Коха. Начальной фигурой для каждого острова является правильный треугольник; фигура на шаге n получается из фигуры, построенной на шаге n - 1, с помощью преобразования каждого отрезка AB этой фигуры в ломаную ACDEB с равными по длине четырьмя звеньями по правилу, показанному на рис. 3.31, где

Рис. 3.31. Преобразование отрезка для троичного острова Коха

Зная координаты концов отрезка AB, нетрудно найти координаты вершин этой ломаной. Обозначим через O начало координат. Положим:

и

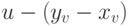
Очевидно, что вектор u перпендикулярен вектору v. Для радиус-векторов вершин C, D и E ломаной имеем:

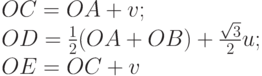
Острова отличаются друг от друга только направлением первого угла поворота, влево или вправо (рис. 3.32 (a-b)). Первый троичный остров называется еще снежинкой Коха.

Рис. 3.32. Троичные острова Коха, n = 4: (a) первый; (b) второй

Очевидно, что представление троичного острова в виде L-системы отличается от представления кривой Коха только аксиомой.

Пример 29. Рассмотрим четверичный остров Коха. Исходной фигурой для построения является квадрат. На шаге итерации каждый отрезок преобразуется в ломаную, состоящую из 8 равных звеньев (рис. 3.33).

Рис. 3.33. Преобразование отрезка четверичного острова Коха